前提共识:研究n阶方阵A
在《黎曼博士的零点》中,对特征值和特征向量有如下描述:特征多项式|λE—A|的根可确定各个特征值λi,
分别计算空间叠加矩阵λiE—A的零空间,该零空间称A的属于λi的特征子空间。
由于特征向量是非零向量,特征子空间的去零向量部分就是属于λi的全体特征向量,
故属于λi的特征子空间的基可代表属于λi的全部特征向量。特征多项式|λE—A|起了什么作用呢?为什么它是求解的钥匙呢?
由于λE表示将单位矩阵的各个正交基都乘了λ倍,与-A叠加后行列式为零,
说明λE使A至少降了1维(含多种情形,可由行列式的性质推想),
由于情形不唯一,因此能起到该效果的λ可能不唯一,
解|λE—A|的根即在于找到全部这样的λi。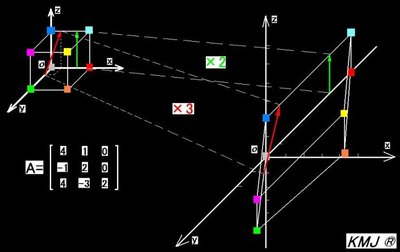
λE对A起如上效果,说明A含有与λ相关的特殊信息。
由于A可视作线性变换,如果它作用到某个非零向量后,仅使该向量伸缩(含倒向及零),
而未转动它(倒向除外),且伸缩系数恰为λi,则该向量为属于特征值λi的特征向量。λiE-A可视作空间行向量的静态组合,其秩为r(λiE-A),
属于λi的特征向量的空间维度便可确定,即n—r(λiE-A)。
由于λi可能存在重根,
当单重时,若n—r(λiE-A)=1,说明该伸缩因子只作用于某1个特殊角度(向量);
当m重时,若n—r(λiE-A)=m,说明分别作用于m个特殊角度的m个伸缩因子等值;
当m重时,若n—r(λiE-A)<m,说明有某m—[ n—r(λiE-A)]个特殊角度法外于该规则。矩阵的对角化,即在找与A相似的一种最简矩阵。
对角阵相当于同阶E的各个正交基各自伸缩一定系数。
例如一个对角阵作用在3维空间内的一个单位立方体时,则线性变换的效果即是沿xyz各轴伸缩,得到新3维体。
若一个n阶方阵A可对角化,即对角阵的各个正交基都须有各自的伸缩因子λi,
则前提是A必须有n个彼此独立的作用角度(特征向量),以便构造n维正交基实现对角化。
下图3阶方阵A只有红绿2个作用方向,伸缩因子分别为3和2,A不可对角化。
顺便一提:若A的某个特征值为0,则0会使属于它的作用方向压扁,属于高维度向低维度投影变换,因此A不可逆。 爱华网
爱华网