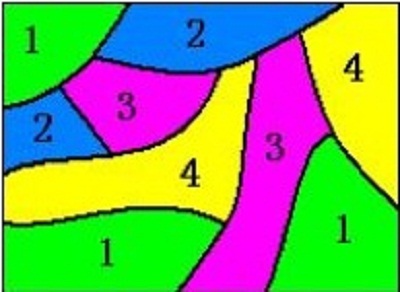
图1.四色地图随着计算机的发展,1976年美国数学家凯尼斯·阿佩尔(K.Appel)和沃夫冈·哈肯(W.Haken)通过两台电子计算机经过1200小时的计算和100亿次的判断,第一次给出了四色 猜想的完全证明,从此,四色猜想成为四色定理。尽管四色猜想通过计算机的强大运算得到了“解决”,但人们对该结果并不满意,因为这个证明过于繁复,类似于枚举证明,不符合数学证明简洁直观的特点。因此,人们也一直致力于寻找更为简洁直观的书面证明。下面,我将介绍我个人这些天对四色问题所做的一点浅显的思考。
地图图形的分类首先,四色猜想中相邻区域指的是两个区域有共边的情形,而不包括两个区域有共点的情形。否者的话,我们可以很容易找到反例,如图2所示,恰如我们所常见的八色雨伞。图2.八色伞这八块区域都相交于中心点,在中心点的情况下,如果也算作相邻,那么,很显然至少要八种颜色。但实际的情况是,任意的交于一点的情况排除于两个区域相邻的情况,而只有相交于一段线的情况下才算作两者相交。于是,上述八个区域至多只需要2种颜色着色就足够了。下面从最简单的情况开始讨论。
多边形之零边形图3.零边形如果在一个平面上只有一个区域,那么很显然,该区域不存在临边的问题,也即该区域只有0条边,这个零边形包括以后的多边形地图的边界我们不妨都以圆来表示,示例区域则以红色来表示。这时的零边形至少需要一种颜色来填充。
多边形之单边形
图4.单边形单边形指该区域与另外的其他区域仅有1条边相邻,这时,无外乎上述三种情况,即该区域完全包含于另一个区域,该区域包含于另一个区域且只有一点相切与另一个区域的边界,该区域与另一区域有一个边相交。事实上,上述三者是等价的。在说明上述三者是等价的之前,先简单介绍一下球极映射。球极映射简单说就是我们可以让球面上的点与平面上的点实现一一映射,同时不改变球面和平面上图形的拓扑结构。图5.球极映射演示球极映射是很有趣的,它即是数学中映射概念的一个特殊实例,同时反映了球面和平面之间深层的关系——二者同是二维的曲面。有了球极映射关系,那么我们可以将上述三种单边形的情况想象在球面上。以单边形(c)为例,它等同于球面上如图6的情况。
图6.单边形(c)球面表示显然红色与橙色仍然相交于一条线段,只不过这条线段是封闭的。而如果我们将图片的换一个角度,从该球形面的左侧观察,同时缩小红色区域与橙色区域的交界区域,于是我们有。
图7.单边形(a)(右)球面表示这时我们得到的上图中右侧的球形图等同于单边形(a)。红色和橙色区域依然只有单条边相交。而如果我们将上图左侧图形按逆时针水平地做一点简单的旋转,我们又有,图8.单边形(b)(右)球面表示不难看出上图8右侧的图形与单边形(b)情况是等价的。红色和橙色区域同样是有一条边相连且有一个点相切。综上,我们就得到了单边形的三种情形是等价的结论。有趣的是,我们还可以通过另一种视角来看这个问题。由单边形(c)不难看出,红色区域与橙色区域二者是等价的,那么单边形(a)和(b)情形中红色和橙色区域是等价的吗?答案是肯定的。
一,我们可以将红色和橙色区域的相交线放大,通过扩大红色区域,缩小橙色区域来实现。这种做法,和上述做法别无二致,只是颜色简单的交换了而已,因此,我们不采用这种颜色等效的方式来实现证明。二,我们可以想象在红色的区域挖一个小洞,从而实现球面向平面的映射,挖一个小洞的目的即让球形区域映射到平面上的是一个有限的区域。如下图9.
图9.球极映射不难看出,这时映射的结果变成了红色区域包裹橙色区域,且二者相交于一条封闭的边,因此红色区域和橙色区域是等价的。另外,我们还可以同时做出红色区域和橙色区域相切于一点的情况,如图10。而如果挖的的洞正在两个区域的交界处,那么我们又有单边形(c)的情况。如图11.图10.球极映射
图11.球极映射在两个单边形彼此相邻的情况下,我们看到至少需要两种颜色填充才能满足彼此颜色不同。
多边形之二边形顺着刚才的思路我们又得到了二边形的各类示例(但请注意,这不是二边形存在的所有的情况,因为它们还有可能与更高阶的多边形相邻),红色区域仍为示例区。
图12.二边形二边形(a)分别和两个单边形相邻,它们整体从形象上看有点像大写的字母“O”。二边形(b)则是一个二边形完全包裹于两个多边形。图13.二边形二边形(c)则是一个二边形与另外两个多(二)边形相切于一点的情形。二边形(d)则说明红色和黄色的区域也是等价的。图14.二边形二边形(e)则明确的告诉我们红、橙、黄三种颜色的区域是等价的,每个都与其他两个区域相邻。事实上二边形(b、c、d、e)这四类情况的红橙黄三色区域都是等价的。在给出它们等价的条件之前,我们先看一下二边形(b)这种情形在球面上是如何显示的。
图15.二边形(b)球面表示上图15,显示的是图二边形(b)在球面上的情形,不难看出,橙色和黄色在二维平面上有两个边相邻和二者在球面上只有一条边相邻是等价的。
图16.二边形(c、d)(右)球面显示我们将上图16中球形沿橙和黄色的临边向上旋转该球,则得到了右侧的图形,易知,右侧图形和二边形(c)和(d)是等价的。下面来说明,上图和二边形(e)的关系。由拓扑性质,我们将上图的圆的红色区域放大,则我们又有图17.二边形(e)(右)球面显示我们便试着从得到的球形的正上侧或正下侧观察该球形,则不难知道,该球形即二边形(e)的球形图像。
图18.二边形(e)球极映射综上,我们就得到了二边形(b、c、d、e)中红橙黄三色区域是等价的。根据球极映射的原理,我们还可以的得到如下的图形也满足红橙黄三色等价。图19.二边形(f)(g)对于上述二边形彼此相邻的情况,至少需要三种颜色才能保证相邻区域彼此颜色不同。
多边形之三边形三边形让我们很容易想到三角形,因为三角形也是三个边的封闭图形。下面,简单列举了一些三边形的构成情形。图20.三边形(a、b)
图21. 三边形(c、d)上图中,三边形(a)为红色区块被三个单边形所围绕,三边形(b)为红色区域被一个单边形和两个二边形所围绕,三边形(c)为一个红色区块,被一个三边形和两个二边形所围绕,三边形(d)显示的则是处于边界三边形情形。
图22.三边形(e、f)三边形(e)和(f)显示的则是4个三边形彼此两两相邻的情形。我们同样地可以将其想象在一个球面上然后通过适当的变形或者由球极映射映射得到三边形两两相邻的另外一些情形。如图23.图23.三边形(g、h、i)三边形(g)同三边形(e、f)所展示的情形恰恰相反,即前者是一个三边形包裹三个三边形,而后者则是三个三边形包裹一个三边形,这是选取不同映射点所引起的结果,前者是一个色块区域的内部,而后者则是三个色块的交界点,这同时也启示我们一种辩证的哲学思维——无穷即零,零即无穷。“空即是色,色即是空”,这里的色不是色情的意思,是有或者物质的意思,即无即是有,有即是无,《红楼梦》中的“假作真时真亦假,无为有处有还无”也体现的是这种辩证的思维。最后,我们注意到这时的三边形四个色块则至少要使用四种颜色才能满足两两相邻且颜色不同的条件。当然,我们还可以画出四边形、五边形甚至更多边形,这里就不再一一列举了。从上面列举的同构图形不难看出,这些等价图形因为映射关系的不同,却可以产生很多不同形态的图形,这让我们处理起来很是棘手。有没有更好的表现形式来表现它们之间的关系呢?当然是有的,这就是多边形图的对偶图。
多边形图之对偶图对偶图即将图形中每个色块看做一个国家,而将每两个相邻国家的首都用线连接起来的所得到的图形即该多边形图的对偶图。对偶图的好处是既保留了图形区块之间原有的拓扑关系,同时又大大简化了出现不同图像的可能。图24.零边至三边形对偶图上图24显示的分别是从零边形到三边形两两相邻情形下的对偶图,这些对偶图更直接的展示了多边形图不同区块间的关系。而同样的代表这些区块的每个顶点,又同样的可以同时放置在一个球面上。若三边形对偶图,所有的节点以及它们的连线构成了一个正三棱锥,而该椎也恰好可以放置在一个球体内,且保证每个锥点都在该球的球面上。另外,因为每两个相邻锥点之间的连线同样的可以紧贴着球面而不会相交。这很好证明,任取一个色块,与它相邻的任意一个色块分布在它的周围,因而,我们可以在与之相邻的任意色块上画一条线,且该线经过两者的临边(无妨从该临边的中间划过),因而我们可以保证这些不同的色块之间任意两条连线都是两两不相交的。如下图所示。图25.对偶图顶点相连示例当然我们也可以让这些多边形进行适当的变形,从而使得彼此之间的连线成为直线段。另外,我们证明一下不可能出现如下的情况,即两条直线在球面上出现相交叉的情况。如下图,
图26.对偶图边相交示例如上图26.所示,红色和橙色区块为相邻区域,两者之间可以画一条线表示二者相邻,而同时,黄色和绿色区域也相邻,它们二者之间也可以画一条线,这时,如果黄色和绿色不相邻于该图形的背面(准确地说是黄绿之间的连线绕过红橙之一的顶点),显然二者是不相邻的,那么二者相邻于该球面的背面,这时我们可以再该球面的背面画一条黄色和绿色的连线,于是这时我们又有红橙和黄绿的连线是彼此不相交的,于是得证,不存在两条色块连线彼此相交的情况。由以上结论知道,该对偶图必然为平面上的简单图(简单图,不存在两条边相交的情况所构成的平面图)。得到了上述结论,我们便可以很好地来解决四色问题。
四色问题的证明顺着图24所给出的对偶图的所提示的规律,我们有如下四边形对偶图。
图27.四边形对偶图如图所示,每个顶点均与其他四个顶点相连,也即每个色块区域都有其他四个四块区域与之相邻,如果这种情况成立的话,那么该图形至少需要五种不同颜色才能够满足彼此两两不同,那么四色猜想也就是错的。但在肯定该结论成立之前,我们应该先证明这个四边形对偶图是平面图形,也即该图的个个顶点可以放置在一个球面上,且不存在两条不同的边在球面上互相交叉的情况。证明:因为BE和AC、AD在平面上相交,为了将上图转换成简单图,我们有如下变形,图28.四边形对偶图这样BE和AC、AD不相交。同样的BD和AC、CE在平面在相交,为了将上图转换成简单图,我们有如下变形,图29.四边形对偶图这时,不难发现,CE和AD仍有一条边相交,为了不让二者相交,我们要么将D点移动至三角形ACE内,要么将E点移动至三角形ACD内,我们无妨将D点移动至三角形ACE内。于是,图30.四边形对偶图尽管,AD与CE不相交了,但BD与AC又产生了相交的关系。对比上两个图,不然发现,二者是同构的,上图的ABCDE同构于下图的DEABC。也就是说,之后的一系列操作都不能使该图形再消减掉一条边,因此该图形不不能构成简单图,也就是四个四边形两两相交的情形在平面或者球面上不存在的,并且对偶图中至少有两条边始终相交。证明二:受证明一的启发。我们可以做如下证明。证明,在三边形对偶图的情形下,第五个顶点,无论它的位于何处,所构成的对偶图都始终至少有两条边相交。这种证法和证明一类似,可以说是异曲同工。这里就不给出证明了。图31.四边形对偶图我们注意到零边形对偶图是零维空间的一个点,一边形对偶图是一维空间的一条线段,二边形对偶图是二维空间的一个平面三角形,三边形对偶图是三维空间的一个正三棱锥,那么四边形对偶图应该是四维空间的超正三棱锥。基于以上规律,我们又有了以下猜想。
N色猜想先来说一下N色猜想的思路。如果是一条直线上不同的边,该边上若干线段以点相隔,那么不难发现一维直线上,至多需要2种颜色就可以区分不同的线段。而四色猜想则可表述为一个平面上有若干区域,这些区域以边相隔,那么这些区域至多只需要4中颜色就可以区分开来。于是,我猜测在三维空间中,同样有若干三维的空间,这些空间之间以面相隔,那么这些区域至多只需要8种颜色就可以区分开来。于是N色猜想为N维空间中,有若干N维的空间区域,这些区域以N-1维的空间区域相隔,那么这些区域至多只需要2^N种颜色就可以区分开来。不幸的是,这个猜想是错误的,至少3维的情况就不满足,当然,这个否定的情况的获得,稍微需哟一点想象力。同样的,我们猜测4维及其以上的情况也不满足。
 爱华网
爱华网