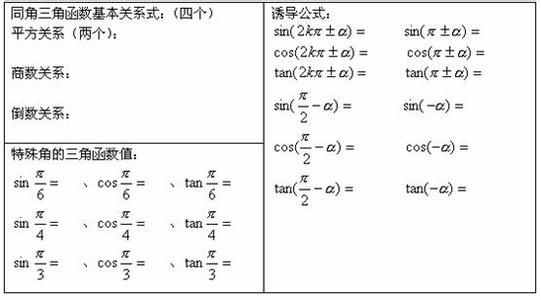
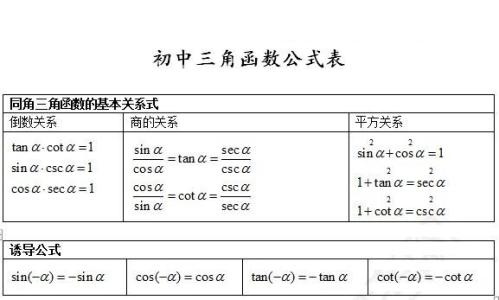
三角函数是高中数学中非常重要的一个知识点,您的孩子掌握了吗?
在教学过程中,我发现很多学生在这一块掌握得还不够牢固,正好昨晚也有学生问到了这方面的知识点,今天我就在这里做一个详细的解析,希望可以帮助更多的学生利用暑假做好查漏补缺的工作!
含有三角函数的代数式称之为三角函数方程,例如sin(mx)=sin(nx),cos(mx)=cos(nx),tan(mx)=tan(nx)这一类就是三角函数方程,除了可以通过变形化成一个或几个简单的三角函数方程求解外,还可以利用如下的结论来求解此类三角函数方程。
1、下面我们先来上述证明结论的正确性,首先证明结论1的充分条件,具体证明过程如下图所示:
(1)结论1:充分性证明过程
2、我们再证明结论1的必要条件,具体证明如下图所示,结论2和结论3的证明与结论1的证明类似,故这里省略了结论2和结论3的证明过程。
3、我们下面来举一个例子来说明如何利用以上结论求解三角函数方程的解,例题如下所示,我们下面用三种不同的方法进行对该例题进行求解。
4、【解法1】Sin2x=1可变形为sin2x=sin(п/2),此时可以利用结论1来求解此方程的解,具体求解过程如下图所示。
5、【解法2】因为sinx=a,其中a的绝对值小于等于1。此方程的解为{x/x=kп(-1)^k*arcsina},具体求解过程如下图所示:

6、【解法3】Sin2x=1,得2x=2kп+п/2,x=kп+п/4,具体求解过程如下图所示:
7、结论
 爱华网
爱华网