一般地,形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
目录
概念性质 特性 定义域与值域第一象限的特殊性图象特别说明展开 概念性质 特性 定义域与值域第一象限的特殊性图象特别说明展开 编辑本段概念 形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。 当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续性的极为深刻的知识。编辑本段性质 (1)、当a>0时,幂函数y=x^a有下列性质: a、图像都通过点(0、0)、(1,1); b、在第一象限内,函数值随x的增大而增大; c、在第一象限内,a>1时,图像是向下凸的;0<a<1时,图像是向上凸的; (2)当a<0时,幂函数y=x^a有下列性质: a、图像都通过点(1,1); b、在第一象限内,函数值随x的增大而减小,图像是向下凸的。特性 对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性: 首先我们知道如果a=p/q,且p/q为既约分数(即p、q互质),q和p都是整数,则x^(p/q)=q次根号下(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。当指数a是负整数时,设a=-k,则y=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道: a小于0时,x不等于0; a的分母为偶数时,x不小于0; a的分母为奇数时,x取R。编辑本段定义域与值域 当a为不同的数值时,幂函数的定义域的不同情况如下: 1.如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根据q的奇偶性来确定,即如果同时q为偶数, 则x不能小于0,这时函数的定义域为大于0的所有实数;2.如果同时q为奇数,则函数的定义域为不等于0 的所有实数。 当x为不同的数值时,幂函数的值域的不同情况如下: 1.在x大于0时,函数的值域总是大于0的实数。 2. 在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。 而只有a为正数,0才进入函数的值域。 由于x大于0是对a的任意取值都有意义的, 因此下面给出幂函数在第一象限的各自情况。编辑本段第一象限的特殊性 可以看到: (1)所有的图形都通过(1,1)这点.(a≠0) a>0时 图象过点(0,0)和(1,1) (2)当a大于0时,幂函数为单调递增为增函数,但y=x^2,在(-∞,0)上单调递减。 而a小于0时,幂函数为单调递减为减函数。 (3)当a大于1时,幂函数图形下凸(竖抛);当a小于1大于0时,幂函数图形上凸(横抛)。当a小于0时,图像为双曲线。 (4)当a小于0时,a越小,图形倾斜程度越大。 (5)显然幂函数无界限。 (6)a=2n,该函数为偶函数 {x|x≠0}。编辑本段图象幂函数
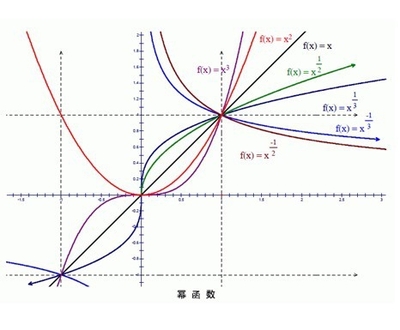
幂函数的图象: ①当a≤-1且a为奇数时,函数在第一、第三象限为减函数 ②当a≤-1且a为偶数时,函数在第二象限为增函数 ③当a=0且x不为0时,函数图象平行于x轴且y=1、但不过(0,1) ④当0<a<1时,函数是增函数 ⑤当a≥1且a为奇数时,函数是奇函数 ⑥当a≥1且a为偶数时,函数是偶函数 幂函数的图像不过第四象限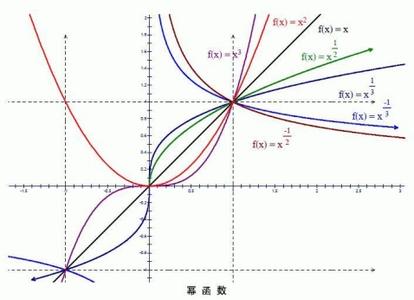
幂函数的九种(2张)编辑本段特别说明 为了研究方便,在初等函数里对于幂函数,只讨论a=1,2,3,1/2,-1时的情形。.bk-album-collection-box{width:687px;height:228px;border:1px solid #c6e1f5;border-top:2px solid #268bd7;margin-bottom:30px;overflow:hidden}.bacb-head{height:28px;background-color:#f5fbff;padding-left:10px;position:relative}.bacb-title{font-size:14px;font-weight:bold;line-height:28px}.bacb-more{text-decoration:none;position:absolute;font-size:12px;line-height:1;line-height:14px 9;top:8px;right:8px;padding-right:9px;padding-right:11px;background:url("http://img.baidu.com/img/baike/s/arr.gif") no-repeat 54px -22px;background-position:54px -23px 9}.bacb-more:hover{text-decoration:none}.bacb-left-btn,.bacb-window-outer,.bacb-right-btn{float:left}.bacb-left-btn,.bacb-right-btn{display:block;text-decoration:none;border:1px solid #FFF;width:17px;height:53px;background:url(http://img.baidu.com/img/baike/bkalbumbtn.gif) no-repeat;cursor:default}.bacb-left-btn{margin:59px 3px 0 6px;_margin-left:3px;background-position:3px 16px}.bacb-right-btn{margin:59px 5px 0 6px;background-position:-27px 16px}.left-enable:hover{background-position:-61px 16px;border:1px solid #DDD;cursor:pointer}.right-enable:hover{background-position:-91px 16px;border:1px solid #DDD;cursor:pointer}.bacb-window-outer{width:628px;height:185px;position:relative;overflow:hidden;margin-top:15px}.bacb-window-inner{position:absolute;top:0;left:0;width:650px;padding-left:6px;_padding-top:1px}.bacb-window-inner .item{float:left;width:156px;height:195px}.bacb-window-inner .img{zoom:1}.bacb-window-inner .img .b1,.bacb-window-inner .img .b2,.bacb-window-inner .img .b3,.bacb-window-inner .img .img-wrapper{background-color:#FFF}.bacb-window-inner .img .b1{border:1px solid #cdcdcd;float:left;position:relative;left:0;top:6px}.bacb-window-inner .img .b2{border:1px solid #cdcdcd;position:relative;left:3px;top:-3px}.bacb-window-inner .img .b3{border:1px solid #AAA;position:relative;left:3px;top:-3px;padding:2px}.bacb-window-inner .img .img-wrapper{left:9px;bottom:9px;display:block;text-decoration:none;line-height:1px}.bacb-window-inner .item .desc{clear:both;display:inline-block;text-align:center;font-family:宋体;width:145px;margin-top:13px;font-size:12px;line-height:1;line-height:14px 9}.bacb-window-inner .item .count{color:#999;white-space:nowrap}词条图册更多图册
幂函数的九种(2张)
词条图片(2张)
扩展阅读: 1注意幂函数与指数函数的区别:幂函数的自变量是底数,指数函数的自变量是指数。
开放分类: 爱华网
爱华网