第17卷 第6期2001年12月雁 北 师 范 学 院 学 报
JOURNALOFYANBEITEACHERS’COLLEGEVol.17No.6Dec.2001
文章编号:100921939(2001)06200011202
求矩阵特征值的两种经典方法
罗 芳1,郑必春2
(11雁北师范学院计算机中心,山西21)
摘 要:.
关键词:旋转变换 Jacobi中图分类号:OA
TWOETHODSOFTAKINGCHARACTERISTICVALUEOFMATRIX
12
LUOFang,ZHENGBi2chun
(1.ComputerCentreofYanbeiTeachers’College.DatongShanxi,037000)
Abstract:Inthispaper,wediscusstwopracticalandclassicalmethodsoftakingcharacteristicvalue,meanwhilepro2
.videacontrastbyexamples
Keywords:rotationtransformation,Jacobimethod,QRmethod
物理、力学和工程技术中的很多问题在数学上都归结为求实对称矩阵的特征值问题,即已知实对称矩阵A=
(aij)n×n,要求代数方程
)=det(Κ f(ΚI-A)=0
的根的问题.当矩阵的阶数为2阶时,我们可以直接解一个二元一次方程而得到A的特征值;但是当n较大时,求解方程
.计算机上常用变换法来计算矩阵全部特det(ΚI-A)=0几乎是不可能的,因而只能通过数值分析方法求得根的近似值
征值,它的理论依据是,将A的特征值问题转化为其相似矩阵B的特征值问题,而转化过程是采用正交相似变换,根据所采用的分解矩阵又分为Jacobi方法与QR方法.
1 Jacobi方法
Jacobi方法的基本思想是通过一组平面为转变换(正交相似变换)将对称矩阵A化为对角矩阵,得其全部特征值.由代数学知道,若A∈Rn×n为对称矩阵,则存在一正交矩阵R,使RART=diag(ΚD,其中D的对角元素Κ1,Κ2,…,Κn)≡i(=
T
1,2,…,n)就是A的特征值,R的列向量Τi就是A的对应Κ.于是求实对称矩阵A的特征值问题在于寻找j的特征向量
T
正交矩阵R,使RAR=D为对角矩阵.下面来简介Jacobi方法的步骤:
令A=A1,于是,依次构造矩阵序列AS,使得 AS+1=R(p,q)AsRT(p,q).
其中,R(p,q)是在(p,q)平面上转过角度Η的一个旋转.在选择平面和确定旋转角度Η中使用的策略是简单的,通过寻求
(S)
AS位于主对角线以上的元素,以确定最大模的项apq(由于考虑到对称性,我们只需要在A的上部的元素中来寻求).然后,选择旋转角Η,使得apq(s+1)=0,利用平面旋转R(p,q)的相似变换仅仅影响位于第p,q行和列的元素.被修改的元素由:
()()()()aips+1=aipscosΗ+aipssinΗ=apsi+1,()()()()
aiqs+1=-aipssinΗ+aiqscosΗ=aqis+1,i≠p,q()()()(s)
(1)apsp+1=apspcos2Η+2apsqcosΗsinΗ+aqqsin2Η,
(s)
2ap(sq)cosΗsinΗ+aqqcos2Η,
()(s)
)=ap(sq+1)apsq+1=(aqq-ap(sp))cosΗsinΗ+ap(s
q)(cos2Η-sin2Η
给出.如果把旋转角Η选择的能消去apq(s+1),那么要求
(
)
()
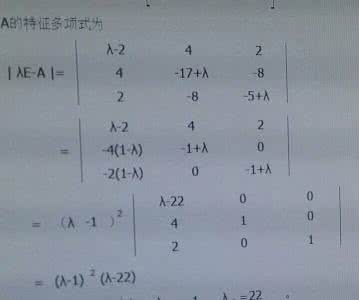
s+1aqq=apspsin2Η-
收稿日期:2001209210
作者简介:罗芳(1970—),女,山西右玉人,讲师,硕士,主要研究计算数学.
(s)
(ap(sp)-aqq).=2ap(sq)??tg2Η
(2)
选择角Η满足:-Π??4≤Η≤Π??4.
(s)(s)
此外,若app-aqq=0,那么选择Η=ap(sq)????ap(sq)???(Π??4).注意,若ap(sq)=0那末就不需要旋转了.(当然按目前的策略,若ap(sq)=0,那末As已经是对角形了.)Jacobi算法产生一个趋向于确定的对角形矩阵的矩阵序列,而这个确定的对角矩阵是与初始矩阵相似的,且这一过程是稳定的,用Jacobi算法最后能得到一个具有一定精度的对角矩阵,因而有RART=0,其中R是平面旋转矩阵的乘积,由于ART=RTD,故RT的各列就是矩阵A的特征向量.
Jacobi方法是一个求对称矩阵A的全部特征值及特征向量的迭代方法,精确度较高,但计算量较大,对稀疏带状矩阵经过平面旋转变换后其稀疏带状将被破坏.
2 QR算法
由代数可知,如果A为非奇异矩阵,则AA进行QR分解:A=QR.于是可得到一新矩阵
B=RQ=QTAQ.
显然,B是由ABA.再对B进行QR分解,又可得到一新矩阵,,s=QsRs,As+1=RsQs定义的.当然,在实际应用中是确定酉阵33
Qs,使QsAs由于Ass=QssAs是彼此U相似的,令A1≡A,进一步,有
33333
As+1ssQs=QsQs-1As-1Qs-1Qs=(Qs…Q1)A1(Q1Q2…Qs)或 Q1Q2sAs+1=A1Q1Q2…Qs,
定义Q(s)=Q1Q2…Qs,R(s)=RsRs-1…R1,则有Q(s)R(s)=Q1…Qs-1QsRsRs-1…R1
=Q1…Qs-1AsRs-1…R1
=A1Q1…Qs-1Rs-1…R1=A1Q(s-1)R(s-1).
最后可得:Q(s)R(s)=As.1
(s)(s)
可见,Q和R给出了As.1的U分解,如果我们要求上三角矩阵Rj的对角元素都是正的,则这一分解是唯一的QR算法有一个非常重要的性质是:如果A1是三对角矩阵,那么所有的矩阵As都是三对角矩阵,且如果A非奇异,则由QR算法产生的{Ak}收敛于对角阵.
例1 求10阶实对称矩阵
20315140156-1714811-4191011315304165.7-1910111214440788.6101.39.12-5.901516750321003.212572.465.783260-6.3-9813-1475
-17.4-18.6100-6.36013145681191032-98135075167-4.9101.3121314754027-
1810119.1257-145162730-421112-5.92.47567-18-4220
解:(1)用Jacobi方法迭代200次求得例的特征值结果见表11
表1 用Jacobi方法求得特征值
K值
Κk
11670514e+01
21748434e+0141173435e+01-6.158298e+0121024783e+02
K值 Κk
-5.741442e-251
31775751e-28621187242e-1011.564298e+265-8,051451e-39
(下转第14页)
12345
678910
并后的链表中,且小者所在链表的下标应后移一个单位,再和未被选中的那个链表的元素比较,以此类推,实现该算法的C程序段如下:
i=1;j=1;k=1;while(i<=a[0]”” j<=b[0])
{if(a[i]<b[i]) {c[k]=a[i];i=i+1;} else{c[k]=b[j];j=j+1;} k=k+1;}
该算法的时间复杂度为0(m+n)第二种情况:
链表中,.
算法1:BA中,:
m=a[n=b[0];i=1;j=1;
while(i<m+n)
{while(a[i]<b[j]) i=i+1;
for(k=i;k<=m+j;k++) {a[k+1]=a[k];} a[i]=b[j];
j=j+1; i=i+1;
}
该算法的时间复杂度为0(m?n)
算法2:从两个链表中选择最大者,存储在A链表中,依次从A链表的m+n号元素开始向前排列,实现该算法的C程序段如下:
n=a[0];m=b[0];k=m+n;a[0]=k;while(n>0 ”” m>0){if (a[n]>b[m])
{[k]=a[];n= [k]=-k1;ile(n>0){a[k]=a[n];n=n-1;k=k-1;}
while(m>0){a[k]=a[m];m=m-1;k=k-1;}
该算法的时间复杂度为0(m+n).
综上所述,在两种情况中,第二种情况较第一种情况运用得多,当m,n趋于无穷大时,两种情况中的算法2的时间复杂度最小.
参考文献
[1]严蔚敏1数据结构[M]1北京:清华大学出版社,19871[2]谭浩强1C程序设计[M]1北京:清华大学出版社,19911[3]谭浩强1BASIC程序设计[M]1北京:高等教育出版社,
19961179—2571
(上接第12页)
(2)用QR方法迭代60次求得例的特征值结果见表21
表2 用QR方法求得特征值
K值12345
Κk
-11091500e+02-61760290e+01-21459404e+01-11633656e+01
K值678910
Κk
41264374e+0161181371e+0171766453e+
0111751596e+0221001009e+02
21762794e+01
由此计算结论可得:当矩阵阶数较高时Jacobi方法求特征值不但迭代次数要求较高,而且精度较低,而QR方法不
但迭代次数要求较少,而且精度也较高.参考文献
[1]李庆杨,王能超,易大义1数值分析[M]1武汉:华中理工大学出版社,19951
[2]A?R?高尔腊伊,G?A?瓦特桑1矩阵特征值问题的计算方法[M]1上海:上海科技出版社,19881
 爱华网
爱华网