立体几何解题技巧 立体几何解题技巧 立体几何预测题

2010年高考数学立体几何（文科）预测题

1.如图，直四棱柱ABCD—A1B1C1D1的高为3，底面是边长为4， 且∠DAB=60°的菱形，AC∩BD=O，A1C1∩B1D1=

E是O1A的中点.

（1）求二面角O1－BC－D的大小； （2）求点E到平面O1BC的距离.

解：建立如图所示的空间直角坐标系O—xyz， ∵底面ABCD是边长为4，∠DAB=60°的菱形， ∴OAOB=2，

则A（23，0，0），B（0，2，0），C（－0，0）， O1（0，0，3）



设平面O1BC的法向量为n1=（x，y，z）， 则n1⊥O1B，n1⊥OC1，

∴

2y3z0

，则z=2，则x=y=3，

3z0

∴n1=3，2），而平面AC的法向量n2=（0，0，3） ∴cos<n1，n2

61

， 342

12设O1－BC－D的平面角为α， ∴cosα=,∴α=60°. 故二面角O1－BC－D为60°. （2）设点E到平面O1BC的距离为d，

1

2

3

∵E是O1A的中点，∴EO1=0，），

2

3

|(3,0,)(,3,2)|

3，∴点E到面O1BC的距离等于3. 则d=|EO1|

2222|n1|2()32

E在CC1上且2. 如图，正四棱柱ABCDA1BC11D1中，AA12AB4，点

C1E3EC．

D（Ⅰ）证明：AC平面BED； 1

（Ⅱ）求二面角A1DEB的大小．

解：以D为坐标原点，射线DA为x轴的正半轴，

1 1

A1

E

A

C

建立如图所示直角坐标系Dxyz．依题设，B(2，2，，0)C(0，2，，0)E(0，21)，，A1(2，0，4)．



DE(0，21)，，DB(2，2，0)，

AC(2，2，4)，DA1(2，0，4)． 1

（Ⅰ）证明 因为ACDB0，ACDE0， 11

故ACBD，ACDE． 11又DBDED， 所以AC平面DBE． 1

（Ⅱ）解 设向量n(x，y，z)是平面DA1E的法向量，则

nDE，nDA1．

故2yz0，2x4z0．

1，2)． 令y1，则z2，x4，n(4，



n，AC等于二面角A1DEB的平面角，

1





． 42

． 42

所以二面角A1DE

B的大小为arccos

3、已知点H在正方体ABCDABCD的对角线B'D上，∠HDA=600． （Ⅰ）求DH与CC所成角的大小； （Ⅱ）求DH与平面AADD所成角的大小．

解：以D为原点，DA为单位长建立空间直角坐标系D

xyz1)(m0) 设H(m，m，则DA(1，0，0)，CC(0，01，)．连结BD，BD．

设DH(m，m，DA60， 1)(m0)，由已知DH，

，DH 由DADHDADHcosDA

可得2mm， 2

00111CC所以DH．（Ⅰ）因为cosDH，， 

CC45．即DH与CC所成的角为45． 所以DH，

（Ⅱ）平面AADD的一个法向量是DC(01，，0)．

01101DC， 所以DH，因为cosDH，DC60． 2可得DH与平面AADD所成的角为30． 

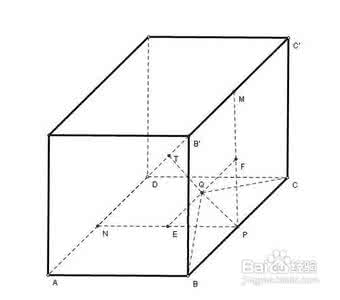
4、 （2008安徽）如图，在四棱锥OABCD中，底面ABCD四边长 为1的菱形，ABC

OA的中点，N4, OA底面ABCD, OA2,M为 为BC的中点

（Ⅰ）证明：直线MN‖平面OCD；

（Ⅱ）求异面直线AB与MD所成角的大小；

（Ⅲ）求点B到平面OCD的距离。

解：作AP

CD于点P,如图,分别以

AB,AP,AO所在直线为

x,y,z

轴建立坐标系

A(0,0,0),B(1,0,0),PD

(O(0,0,2),M(0,0,1),

N(1,

2(1)证明

MN(1,1O),P,,O2D),, 44222,2)

设平面OCD的法向量为n(x

,y,z),则nOP0,nOD

y2z

02即 

xy2z0

取

z

解得n



∵MNn(11)0 MN‖平面OCD

1) (2)解 设AB与MD所成的角为,∵AB(1,0,0),MD(ABMD1 ∴cos, , AB与MD所成角的大小为. ∴3

3ABMD2

(3)解 设点B到平面OCD的距离为d，

则d为OB在向量n上的投影的绝对值,

OBn22.所以点B到平面OCD的距离为 由 OB(1,0,2), 得d3n3

爱华网本文地址 » http://www.aihuau.com/a/315151/360704114565.html