yinci fenxi
因次分析
dimensional analysis
又称量纲分析,是对过程有关物理量的因次(即量纲)进行分析,得到为数较少的无因次数(即无量纲参数)群间关系的方法,和相似论方法同为指导实验的化学工程研究方法,在工程学科的研究中有着广泛的应用。
方法基础 ①很多物理量都是有因次的,如速度的因次为(长度/时间),写作LT,密度的因次为(质量/长度),写作ML等。若干物理量总能以适当的幂次组合构成无因次的数群,如在研究管内流动时,可将速度 、管径、流体密度,流体粘度 四个量组成一个无因次数群/,即雷诺数。②任何物理方程总是齐因次的,即相加或相减的各项都有相同的因次。因此原则上,经过适当的变换,物理方程总可以改写为无因次数群间关系的形式。
定理 定理是由任何物理方程都是齐因次的这一事实推出的。此定理指出:对一特定的物理现象,由因次分析得到无因次数群的数目,必等于该现象所涉及的物理量数目与该学科领域中基本因次数之差。例如,在研究流体在光滑水平直管中作定态流动的流动阻力时,根据对这一物理现象的了解,已经知道压力损失与管径、管长、流速、流体密度、流体粘度有关,这种关系可用如下函数表示:
=(,,,,) (1)该物理现象共涉及六个物理量。在力学中基本因次通常为长度、时间和质量,因而根据定理可将式(1)变成三个无因次数群间的关系:
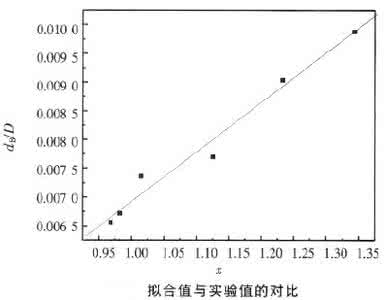
[745-01] (2)式中/()为欧拉数;/为简单几何数群。这样在实验研究中便不需要测定各个物理量之间的定量关系,而只需测定上述无因次数群间的函数关系。
方法特点 这种方法有两个优点:①变量数减少了,实验工作量可以减少;②由于只需逐次改变无因次数群的值,而不必逐个改变各物理量的值,实验工作可以大大简化。例如,在上述关于流动阻力的研究中,为改变雷诺数(/)的值,原则上只需改变流速,既不需改变管径,也不需更换流体以改变流体性质和,所得实验结果可同样有效地用于其他管径和其他流体。
与相似论相比,因次分析方法不需要先列出描述过程的微分方程式,只需事先确定有关物理量。因此,因次分析方法的应用范围较相似论广。但是因次分析方法并不能指出哪些物理量是有关的和必要的,若过多地引入了一些关系不大的物理量,常常会增加分析上的复杂性;若遗漏了实际上有关的物理量(特别是当过程涉及无因次的物理量时),则可能导致严重的失误。
陈敏恒
以上就是网友分享的关于"因次分析"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网