一、对酒当歌,人生几何。
这句话的意思是说,人生最快乐的事情,就是学几何(纯属歪读,不要当真)。学到开心处,自是放歌时。刷几何题刷到兴起,忍不住就要大喝一口酒,山歌儿唱一首!(酗酒有害,切勿模仿!)
学而思有个紫包菜老师,自称几何之王。每次上课上到几何的内容,都要大喊一声:这个让我来!
几何的魅力可见一斑。
先看看,我们小学学习哪些几何内容?
小学几何内容大体划分为两大块,平面几何和立体几何。平面几何又包括平面直线和平面曲线。具体如下:
果然是一大家子!内容相当多啊!
现在,咱们把眼光聚焦在五年级:五年级,是整个小学几何内容集大成的年级!
为什么这么说?
1、因为五年级,我们会结束直线几何的学习:直线几何考察最多的比例模型、勾股定理,都在五年级学完!
2、因为五年级,我们会开启平面曲线的学习,完善平面几何内容:这个寒假,第五讲,圆与扇形初步,在此基础上,春季学习圆与扇形进阶。
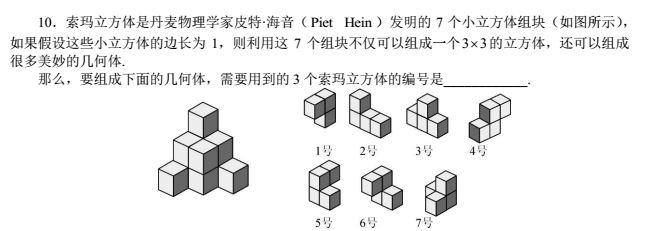
3、因为五年级,我们会掀开几何世界的另一扇门:立体几何。这个寒假,第一讲,长方体与正方体,学习基本的表面积与体积问题,在此基础上,春季学习三视图(立体图形与几何想象)。
五年级学完,小学几何内容基本就搞定了,六年级,也就是旋转与轨迹、圆柱圆锥球这些扫尾工作了。
二、几何如此美妙,杯赛怎么能少?
紫包菜曾经曰过:哪个杯赛不考几何,它就一定不是一个正规的杯赛!
跃跃欲试拿着这个标准去考核了各大杯赛,发现他们真的都好正规!你看,走美杯、希望杯、华杯赛、启智杯、学而思杯,没有一个不考几何的!
就说说咱们五年级寒假两讲(正方体与长方体、圆与扇形)吧,就足足考了这么多:
2015华杯赛高年级组(五六年级)决赛:长方体的体积问题
2015希望杯五年级初赛:正方体长方体的表面积、体积问题
2015希望杯五年级初赛:三视图问题
2015希望杯五年级初赛:正方体长方体的表面积、体积问题
2015希望杯五年级决赛:长方体表面积与体积问题,结合质数合数的数论知识。
2015走美杯五年级:三视图问题
2015学而思杯五年级:三视图问题
2014启智杯:圆的面积,结合比例思想。
咦,怎么启智杯是2014年的?跃跃欲试打错了?还是没找到2015年的试卷?答案是后者——我没找到2015年启智杯的试卷。因为还在深圳市初等数学学会那里存着呢,11月29日才会跟大家见面。顺便提醒,报名的别忘了去考哦!
2015走美杯五年级:圆的面积问题
总结起来一句话,
必须要学此寒假。
要是不学就完啦,
别人发笑你犯傻!
(脑筋出了点问题,见谅……)
三、杯赛升学一定考,多少孩子竟折腰?
1、基础不牢,地动山摇。
很多孩子之前没接触过比例思想,没学过比例模型,秋季学鸟头模型,简直痛苦得欲生欲死。即使是学过的,如果对于比例思想没有很好的理解,也会时不时犯浑。试想,为了达到直线几何的制高点,我们做了多少铺垫?四年级春季:等积变形、一半模型;五年级暑假:比和比例、比例模型,这才一路走到秋季的三个吉祥物:蝴蝶、鸟头、燕尾。如果前面的没学,秋季遭点罪,难道不是应该的么?赶紧补上来,为时未晚。
所以,基础很重要。千万不要让知识断层!
2、模型教学是根本大计
几何题,考察孩子的观察能力和抽象思维能力,先要仔细观察题目给的边边点点,然后寻找可用条件,再去搭建条件与问题之间的联系,想想都恐怖。而小学生的抽象读图能力本身是比较弱的(毕竟几何图形不是画个猫猫狗狗,一看就懂)。小学阶段,就是要培养孩子的读图能力,我们的方式叫“模型教学”:就是通过总结一类具有共同特征的模型,帮孩子识别图形特征,进而找到解决问题的套路。到了初高中以后,就着重培养孩子的推理论证能力了。
小学要想学好直线几何,必须熟悉各个模型,熟知每个模型的特征,能熟练运用每个模型的结论。要实现这个目标,非多做多练不可。
3、空间想象能力很关键
这个真有点拼天赋了。对于展开图、三视图问题,有的孩子一点就通,有的孩子怎么学都晕,这个确实跟孩子的天赋有点关系。有的孩子大约小时候积木玩的多,空间想象能力强,有的孩子弱一点,那也急不得。
擅长的,多钻研;不擅长的,多联系,勤能补拙是实话!
 爱华网
爱华网