B.
C.
D.
题型:多选题难度:偏易来源:广东
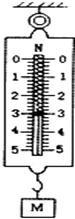
由图可知,t0至t1时间段弹簧秤的示数小于G,故合力为G-F=50N,物体可能向下加速,也可能向上减速;
t1至t2时间段弹力等于重力,故合力为零,物体可能为匀速也可能静止;
而t2至t3时间段内合力向上,故物体加速度向上,电梯可能向上加速也可能向下减速;
AD均符合题意;
故选AD.
考点:
考点名称:匀变速直线运动定义:
在任意相等的时间内速度的变化相等的直线运动,即加速度恒定的变速直线运动叫匀变速直线运动。
特点:
a=恒量。
匀变速直线运动规律(基本公式):
速度公式:v=
位移公式:x=
速度平方公式:
位移—平均速度关系式:x=
匀变速直线运动的几个重要推论:
在任意两个连续相等的时间间隔内通过的位移之差为一恒量,即:SⅡ-SⅠ=SⅢ-SⅡ=…=SN-SN-1=ΔS=(此公式可以用来判断物体是否做匀变速直线运动)。进一步推论:Sn+m-Sn=,其中Sn、Sn+m分别表示第n段和第(n+m)段相等时间内的位移,T为相等时间间隔。某段时间内的平均速度,等于该段时间的中间时刻的瞬时速度,即。某段位移中点的瞬时速度等于初速度v0和末速度v平方和一半的平方根,即vs/2=。考点名称:牛顿第二定律内容:物体的加速度跟所受的外力的合力成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同,表达式F=kma。在国际单位制中,k=1,上式简化为F合=ma。牛顿这个单位就是根据牛顿第二定律定义的:使质量是1kg的物体产生1m/s2加速度的力,叫做1N(kg·m/s2=N)。
对牛顿第二定律的理解:
①模型性
牛顿第二定律的研究对象只能是质点模型或可看成质点模型的物体。
②因果性
力是产生加速度的原因,质量是物体惯性大小的量度,物体的加速度是力这一外因和质量这一内因共同作用的结果。
③矢量性
合外力的方向决定了加速度的方向,合外力方向变,加速度方向变,加速度方向与合外力方向一致。其实牛顿第二定律的表达形式就是矢量式。
④瞬时性
加速度与合外力是瞬时对应关系,它们同生、同灭、同变化。
⑤同一性(同体性)
中各物理量均指同一个研究对象。因此应用牛顿第二定律解题时,首先要处理好的问题是研究对象的选择与确定。
⑥相对性
在中,a是相对于惯性系的而不是相对于非惯性系的,即a是相对于没有加速度参照系的。
⑦独立性
F合产生的加速度a是物体的总加速度,根据矢量的合成与分解,则有物体在x方向的加速度ax;物体在y方向的合外力产生y方向的加速度ay。牛顿第二定律分量式为:。
⑧局限性(适用范围)
牛顿第二定律只能解决物体的低速运动问题,不能解决物体的高速运动问题,只适用于宏观物体,不适用与微观粒子。牛顿第二定律的应用:
1.应用牛顿第二定律解题的步骤:
(1)明确研究对象。可以以某一个质点作为研究对象,也可以以几个质点组成的质点组作为研究对象。设每个质点的质量为mi,对应的加速度为ai,则有:F合=
对这个结论可以这样理解:先分别以质点组中的每个质点为研究对象用牛顿第二定律:,将以上各式等号左、右分别相加,其中左边所有力中,凡属于系统内力的,总是成对出现并且大小相等方向相反,其矢量和必为零,所以最后得到的是该质点组所受的所有外力之和,即合外力F。。
(2)对研究对象进行受力分析,同时还应该分析研究对象的运动情况(包括速度、加速度),并把速度、加速度的方向在受力图旁边表示出来。
(3)若研究对象在不共线的两个力作用下做加速运动,一般用平行四边形定则(或三角形定则)解题;若研究对象在不共线的三个或三个以上的力作用下做加速运动,一般用正交分解法解题(注意灵活选取坐标轴的方向,既可以分解力,也可以分解加速度)。
(4)当研究对象在研究过程的小同阶段受力情况有变化时,那就必须分阶段进行受力分析,分阶段列方程求解。
2.两种分析动力学问题的方法:
(1)合成法分析动力学问题若物体只受两个力作用而产生加速度时,根据牛顿第二定律可知,利用平行四边形定则求出的两个力的合力方向就是加速度方向。特别是两个力互相垂直或相等时,应用力的合成法比较简单。
(2)正交分解法分析动力学问题当物体受到两个以上的力作用而产生加速度时,常用正交分解法解题。通常是分解力,但在有些情况下分解加速度更简单。
①分解力:一般将物体受到的各个力沿加速度方向和垂直于加速度方向分解,则:(沿加速度方向),(垂直于加速度方向)。
②分解加速度:当物体受到的力相互垂直时,沿这两个相互垂直的方向分解加速度,再应用牛顿第二定律列方程求解,有时更简单。具体问题中要分解力还是分解加速度需要具体分析,要以尽量减少被分解的量,尽量不分解待求的量为原则。
3.应用牛顿第二定律解决的两类问题:
(1)已知物体的受力情况,求解物体的运动情况解这类题目,一般是应用牛顿运动定律求出物体的加速度,再根据物体的初始条件,应用运动学公式,求出物体运动的情况,即求出物体在任意时刻的位置、速度及运动轨迹。流程图如下:
(2)已知物体的运动情况,求解物体的受力情况解这类题目,一般是应用运动学公式求出物体的加速度,再应用牛顿第二定律求出物体所受的合外力,进而求出物体所受的其他外力。流程图如下:
可以看出,在这两类基本问题中,应用到牛顿第二定律和运动学公式,而它们中间联系的纽带是加速度,所以求解这两类问题必须先求解物体的加速度。知识扩展:
1.惯性系与非惯性系:牛顿运动定律成立的参考系,称为惯性参考系,简称惯性系。牛顿运动定律不成立的参考系,称为非惯性系。
2.关于a、△v、v与F的关系
(1)a与F有必然的瞬时的关系F为0,则a为0; F不为0,则a不为0,且大小为a=F/m。F改变,则a 立即改变,a和F之间是瞬时的对应关系,同时存在,同时消失.同时改变。
(2)△v(速度的改变量)与F有必然的但不是瞬时的联系 F为0,则△v为0;F不,0,并不能说明△v就一定不为0,因为,F不为0,而t=0,则△v=0,物体受合外力作用要有一段时间的积累,才能使速度改变。
(3)v(瞬时速度)与F无必然的联系 F为0时,物体可做匀速直线运动,v不为0;F不为0时,v可以为0,例如竖直上抛到达最高点时。
 爱华网
爱华网