关键词:DBSCAN 大规模数据集 分类属性数据
中图分类号:TP301.6 文献标识码:A 文章编号:1007-9416(2016)11-0134-01
1 引言
基于密度的DBSCAN聚类算法可以在含有噪声的空间数据库中发掘随意不同形状的簇,但前提条件是要用户给定密度阈值,将空间对象中含有高密度的区域划分为簇[1]。密度阈值有两个参数构成,其中为半径参数,MinPts为以为半径的领域内至少包含对象的最小数量。这两个参数需要事先根据经验人为确定,所以就导致算法对参数敏感,最终的聚类结果也会因为参数的细微变化产生较大的差异。为了克服DBSCAN算法所存在的上述缺点,海内外许多研究学者已经相继提出了一些改良方法。其中OPTICS算法就是通过生成有序队列表优化Eps参数值;AGD-DBSCAN算法就是利用数据集特点来确定Eps、MinPts这两个参数等[2]。
DBSACAN聚类算法需要逐个寻找中心节点并且根据迭代明确全部密度可达对象,这就造成该算法的时间复杂度是。若算法采取空间索引,该算法的时间复杂度是,其中是数据库中对象的数量。DBSCAN算法的时间复杂度与数据集接近线性关系,可知它可以有效地处理大规模数据集,该算法能够有效的处理数值型数据,但在大规模数据集上不能处理混合型数据。为了克服上述这一缺点,本文提出了一种两阶段的聚类整合算法(TDBSCAN)。该算法第一阶段,采用一趟聚类算法初步划分原始数据集,将非常靠近的对象当作同个整体对待,对原始数据集实行紧缩表示;第二阶段,使用现有的DBSCAN聚类算法合并初步划分获得最后的聚类结果。最后通过实例验证该算法可以很好地解决含有混合属性的大规模数据集的聚类问题。
2 基于DBSCAN聚类算法的改进
2.1 相关定义
定义1簇与间的距离定义为,这里每条记录有个属性,此中有个分类属性和个数值属性,为与在属性上的不同。分类属性其值是定义与中对象在属性上的距离均值:
这里,是中两个对象。对于数值属性,。和分别为和对应属性的质心。
原始DBSCAN聚类算法可以处理数值属性数据,但无法处理含分类属性数据,定义1[3]可运算分类属性数据之间的距离,采用定义1代替欧式距离对原始DBSCAN进行拓广,使之能处理分类属性数据。
2.2 DBSCAN聚类算法的改进设计
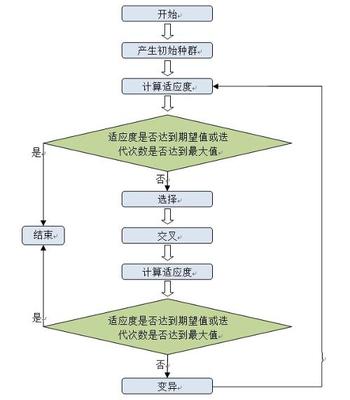
TDBSCAN算法的聚类过程如下:
Stage1.初始聚类的划分
1)开始时,采用一趟聚类算法将数据集D分割成同样大小的k个簇,簇集合为空,各个簇输入一个新的对象。
2)以这个对象去构建一个新的簇。
3)如已到数据集的尾端,则转到(5),不然输入新对象采用上述的距离定义运算它与各个已有簇间中心对象的距离,然后选取最短距离。
4)若最短距离大于给出的阈值r转(2),不然将该对象读入最短距离的簇中并跟新簇的质心,转(3),其中阈值r的取值在之间,和为过程2)中每个对象之间距离的平均值和方差。
5)结束。
Stage2.DBSCAN聚类过程
6)将上一阶段获得的每个簇看作一个对象,然后采用现有的DBSCAN聚类算法进行聚类归并。
3 实验分析
3.1 实验环境
实验所用到的计算机的配置为windows10旗舰版操作系统,Intel i3 双核处理器,4GHz主频和4GB内存,实验数据采用Mushroom数据集和KDDCUP99数据集,算法是用Java语言在Eclipse软件上进行编写所实现。
3.2 实验结果分析与比较
K-prototypes算法[4]涵盖了K众数划分聚类和K均值划分聚类这两个算法的不同特点,可以有效地处理混合属性数据。将TDBSCAN算法与K-prototypes算法在Mushroom数据集和KDDCUP99数据集上就聚类精度[5]进行比较。Mushroom数据集约含有8000多条记录,每条记录都有22个分类属性来描述的。KDDCUP99数据集约含有四百九十多万条模拟记录,每条记录由34个数值型属性和7个分类属性所描述,选用一个大概5%的数据子集来检测算法,该子集包括正常记录和攻击记录。在选定的数据集上重复运行5次,每次都要随机改变记录的顺序,实验结果如表1所示。
测验结果表明TDBSCAN算法在上述2个选定的数据集上的平均聚类精度分别高于K-prototypes算法大约4%和5%,聚类的稳定性也比较好。
4 结语
针对DBSCAN聚类算法在大规模数据集上存在无法处理混合属性数据的难题,本文提出了一种两阶段的聚类整合算法。通过实例验证该算法可以很好地处理含有混合属性的大规模数据集的聚类问题,并且较其他算法在平均聚类精度和聚类的稳定性上有所提高。
参考文献
[1]Jiawei Han, Micheline Kamber. Data mining conepts and techniques[M]. Beijing: China Machines Press.2001:273-274.
[2]陈刚,刘秉权,吴岩.一种基于高斯分布的自适应DBSCAN算法[J].微电子学与计算机,2013,30(3):27-30.
[3]蒋盛益,罗方伦,余雯.基于视觉原理的密度聚类算法的改进[J].山东大学学报,2011,41(4):86-90.
[4]Huang Zhexue.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery,1998,2(3):283-304.
[5]孙浩军,闪光辉,等.一种高维混合属性数据聚类算法[J].计算机工程与应用,2015,51(8):128-133.
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网