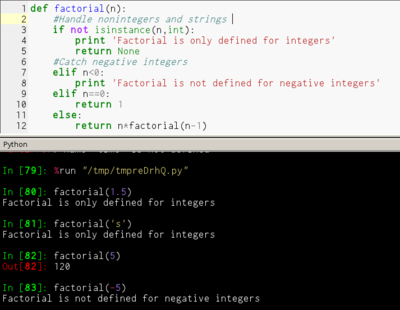
如果一个函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归。尾递归函数的特点是在回归过程中不用做任何操作,这个特性很重要,因为大多数现代的编译器会利用这种特点自动生成优化的代码。
当编译器检测到一个函数调用是尾递归的时候,它就覆盖当前的活跃记录而不是在栈中去创建一个新的。编译器可以做到这点,因为递归调用是当前活跃期内最后一条待执行的语句,于是当这个调用返回时栈帧中并没有其他事情可做,因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。因此,只要有可能我们就需要将递归函数写成尾递归的形式。
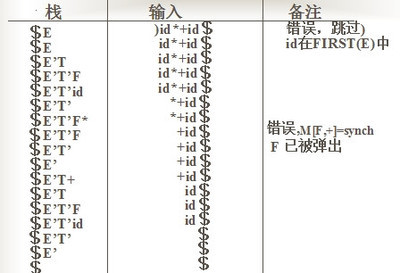
为了理解尾递归是如何工作的,让我们再次以递归的形式计算阶乘。首先,这可以很容易让我们理解为什么之前所定义的递归不是尾递归。回忆之前对计算n!的定义:在每个活跃期计算n倍的(n-1)!的值,让n=n-1并持续这个过程直到n=1为止。这种定义不是尾递归的,因为每个活跃期的返回值都依赖于用n乘以下一个活跃期的返回值,因此每次调用产生的栈帧将不得不保存在栈上直到下一个子调用的返回值确定。现在让我们考虑以尾递归的形式来定义计算n!的过程。函数可以定义成如下形式:
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=51 alt="" src="http://pic.aIhUaU.com/201602/15/1019380.jpg" width=449 border=0>[/TD][/TR]这种定义还需要接受第二个参数a,除此之外并没有太大区别。a(初始化为1)维护递归层次的深度。这就让我们避免了每次还需要将返回值再乘以n。然而,在每次递归调用中,令a=na并且n=n-1。继续递归调用,直到n=1,这满足结束条件,此时直接返回a即可。图3-4说明了用尾递归计算4!的过程。注意在回归的过程中不需要做任何操作,这是所有尾递归函数的标志。
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=174 alt="" src="http://pic.aIhUaU.com/201602/15/1019381.jpg" width=458 border=0>[/TD][/TR]
[TR]
[TD]图3-4:以尾递归的方式计算4![/TD][/TR]
代码实例3-2给出了一个C函数facttail,它接受一个整数n并以尾递归的形式计算n的阶乘。这个函数还接受一个参数a,a的初始值为1。facttail使用a来维护递归层次的深度,除此之外它和fact很相似。读者可以注意一下函数的具体实现和尾递归定义的相似之处。
示例3-2:以尾递归的形式计算阶乘的一个函数实现
/*facttail.c*/ #include"facttail.h" /*facttail*/ intfacttail(intn,inta){ /*Computeafactorialinatail-recursivemanner.*/ if(nreturn0; elseif(n==0) return1; elseif(n==1) returna; else returnfacttail(n-1,n*a); }
示例3-2中的函数是尾递归的,因为对facttail的单次递归调用是函数返回前最后执行的一条语句。在facttail中碰巧最后一条语句也是对facttail的调用,但这并不是必需的。换句话说,在递归调用之后还可以有其他的语句执行,只是它们只能在递归调用没有执行时才可以执行。图3-5展示了当使用尾递归函数计算4!时栈使用的情况,读者可以和图3-3展示的栈使用情况作对比。
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=252 alt="" src="http://pic.aIhUaU.com/201602/15/1019382.jpg" width=564 border=0>[/TD][/TR]
[TR]
[TD](点击查看大图)图3-5:以尾递归形式计算4!时栈的情况[/TD][/TR]
 爱华网
爱华网