偏导数
partial derivative
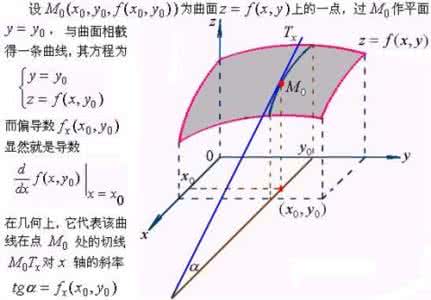
二元函数z=f(x,y)沿坐标轴方向的方向导数(或沿坐标轴方向的变化率)。即把z=f(x,y)中的一个自变量y看作常数,于是z=f(x,y)就成为关于x的一元函数,给x以改变量Δx,则有z关于x的(偏)改变量Δxz=f(x+Δx,y)-f(x,y),如果极限(存在且有限,就称此极限为二元函数 z =f( x,y )在 P(x,y)点关于x的偏导数,记作,或(x,y),类似地有因此 ,计算二元函数的偏导数可按照一元函数的求导法则和公式进行 。例如,z=x2+y2+1,又如,以上就是网友分享的关于"偏导数"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
爱华网本文地址 » http://www.aihuau.com/a/342351/896883111958.html
更多阅读

对不起,暂不支持该格式!

原文地址:矩阵求导公式【转】作者:三寅今天推导公式,发现居然有对矩阵的求导,狂汗--完全不会。不过还好网上有人总结了。吼吼,赶紧搬过来收藏备份。基本公式:Y = A * X --> DY/DX = A'Y = X * A --> DY/DX = AY = A' * X * B --> DY/DX =

两个物体从两地出发,相向而行,经过一段时间,必然会在途中相遇,这类题型就把它称为相遇问题。相遇问题是研究速度,时间和路程三者数量之间的关系。相遇问题除了要弄清路程,速度与相遇时间外,在审题时还要注意一些重要的问题:是否是同时出发,

植树问题通常是指沿着一定的路线植树,这条路线的总长度被树平均分成若干段,由于路线不同、植树要求不同,路线被分成的段数和植树的棵数之间的关系就不同,存在着“总距离÷间隔距+1=棵数、总距离÷间隔距=棵数、总距离÷间隔距
用符号表示物理量,用式子表示几个物理量之间的关系。是物理规律的简洁反映。例如微波辐射电磁能量,向空间传播,在任意距离r处的功率密度为:s=P/(4πr)^2, w/m^2,电视直播卫星的EIRP大约在15dBw左右,通常地面卫星电视的频率为4千兆或12千兆

 爱华网
爱华网



