几何分布的期望和方差几何分布-爱华网

几何分布

几何分布(geometric distribution)是离散型机率分布。描述第n次伯努利试验成功的机率。详细的说，是： n次伯努利试验，前n-1次皆失败，第n次才成功的机率。

公式：

看图片——————>

期望值：

1/p

方差：

（1-p）/p*p

以上就是网友分享的关于"几何分布"的相关资料，希望对您有所帮助，感谢您对爱华网的支持！

方差和标准差的年化问题方差标准差协方差

现有一个投资组合，假定该组合的日收益率序列用250（一年按250个交易日）个变量表示：，并且假定这250组观测值独立同分布，那么可以计算该投资组合的年化方差和年化标准差。首先，年化方差和年化标准差的统计对象为年化收益率变量，所以我们首先构

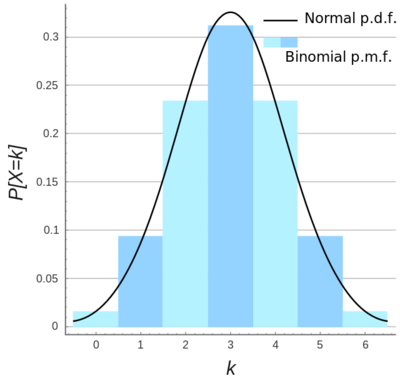
1.数学期望设离散随机变量的概率分布为P(=xi)=p(xi),(i=1,2,...),若其函数η=f(ξ),则随机变量η的数学期望定义为2.泊松分布

《几何原本》的意义和影响在几何学上的影响和意义在几何学发展的历史中，欧几里得的《几何原本》起了重大的历史作用。这[欧几里得]欧几里得种作用归结到一点，就是提出了几何学的“根据”和它的逻辑结构的问题。在他写的《几何原本》中

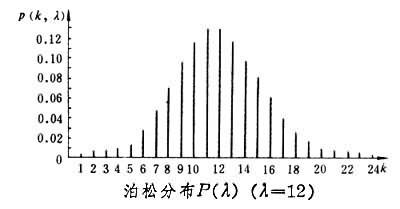
设随机变量　　，则再计算　　，故一、Poisson分布的概念Poisson分布更多地专用于研究单位时间、单位人群、单位空间内，某罕见事件发生次数的分布。如某种细菌在单位容积空气或水中出现的情况，某段时间特定人群中某种恶性肿瘤患者的分布或

这篇文章总结了概率统计中期望、方差、协方差和相关系数的定义、性质和基本运算规则。期望定义设是一个离散概率分布函数，自变量的取值范围为。其期望被定义为：设是一个连续概率密度函数。其期望为：性质1、线性运算