昨天下午一位85岁的老校长(刘梦经)带来他做的数学题--“拿破仑三角形”的证明给我看。使我夫妇大吃一惊。他是1963年,我大学毕业首个工作岗位,蚌埠三中的副校长,后来调市计量局,任副局长。解放前大学毕业,是我们老前辈,退休多年,至今仍然用数学题锻炼思维,身体十分健壮。他分别用平面几何,解三角形,解析几何三种数学方法证明著名数学问题“拿破仑三角形”,思维清晰,非常值得我们学习。
本文先介绍拿破仑三角形是什么,以后再发表他的解法。
拿破仑定理与拿破仑三角形
在任意△ABC的外侧,分别作等边△ABD、△BCE、△CAF,则AE、BF、CD三线共点X,并且AE=BF=CD,如下图。这个命题称为拿破仑定理。
【定义1】外拿破仑三角形
以△ABC的三条边分别向外作等边△ABD、△BCE、△CAF,它们的外接圆⊙P 、⊙Q 、⊙R 的圆心构成的三角形。
如下图
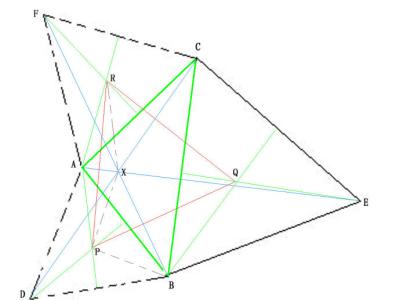
可以证明:外拿破仑三角形是一个等边三角形。
还可以证明:点X是外接圆⊙P 、⊙Q 、⊙R 三圆的共点。
【定义2】内拿破仑三角形
ABC的三条边分别向△ABC的内侧作等边△ABD、△BCE、△CAF,它们的外接圆⊙P 、⊙Q 、⊙R 的圆心构成的三角形
同样可以证明:内拿破仑三角形也是一个等边三角形,外接圆⊙P 、⊙Q 、⊙R共点。
拿破仑三角形还可作如下推广:
1、原三角形的面积等于它的外、内拿破仑三角形面积之差。
2、原三角形的重心也是内和外拿破仑三角形的重心。
3、以△ABC的三边为边分别向三角形外侧作三个相似的三角形ABC′、CA′B、B′CA,(相似三角形的顶点对应排列)这三个三角形的外心为 P、Q、R,则△PQR也与这三个三角形相似。
外拿破仑三角形即为此题之特例,这只要让三个相似三角形是正三角形即可。 爱华网
爱华网