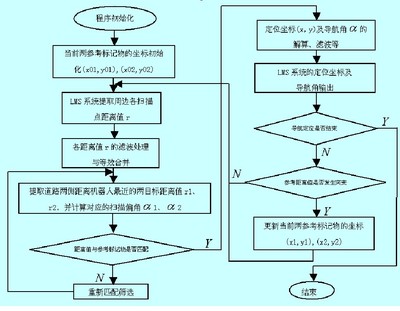
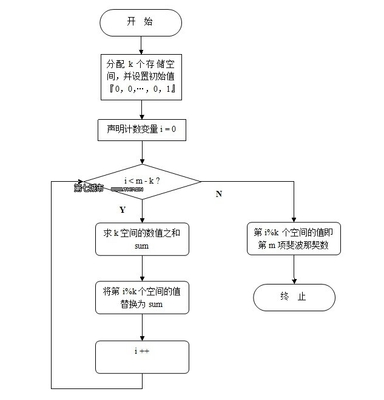
数列是高考必不可少的一个知识点，这周我们就来讲一类数列通项式的求解方法:高中遇到的数列，绝大多数可以转化为求和数列与求积数列，典型数列分别为等差数列和等比数列。
先看看我们会遇到这种类型的题，以简单的数字举例，之后我们从基本形式开始说起，怎么得到下面的几种复杂形式，以及如何再由复杂形式，转变成基本形式以方便做题。
递推关系式—由基础演变得来
递推关系式—由基础变形得来
还有其他形式吗？当然有，在这不做过多介绍。
还有其他求通项式的方法吗？完全归纳也许是个不错的选择！
学会了求通项式的一般思路，考试中遇到不常见的形式，一般会有相应的提示，我们按照提示配凑就可以，周五我们会拿一道15年的高考题来说说。
今天先练习两个简单的习题，
简单题，步骤很重要，步骤很重要，步骤很重要！
如何由数列的递推公式求通项？徐辉知数列的递推公式求其通项是高中数学的重要内容，也是高考数学的重点、热点和难点内容之一，这部分内容往往会作为比较难的题目出现，需要结合函数知识，通过引入辅助数列，利用等差等比数列的定义，综合应用迭加
一、分母含等差数列且分子为常数的裂项⑴ 一般形式（一阶）通项⑵ 多阶形式多阶一般式通项二、分母中含特殊乘式的裂项⑴ 伪等比形式可以看出，若分母两乘式之差不是定值，则分子一定是与其差类似（一般与n有关）的结构，不然可能无法裂项
递推最小二乘参数估计(RLS)考虑如下系统：式中x(k)为方差为0.1的白噪声。clear all; close all;a=[1 -1
--
对全微分表示式求积分的一般方法陈建一设有函数f=g(x1，x2，…，xn)<1><1>式两边对x1 求偏导数，有〆f/〆x1=〆g/〆x1 +(〆g/〆x2)(〆x2/〆x
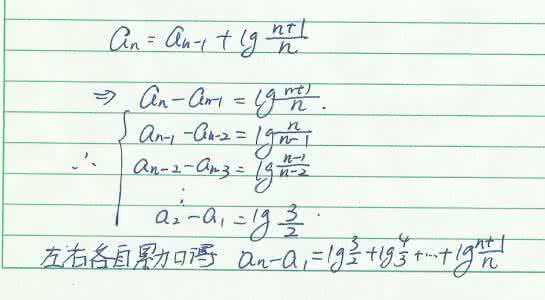
爱华网