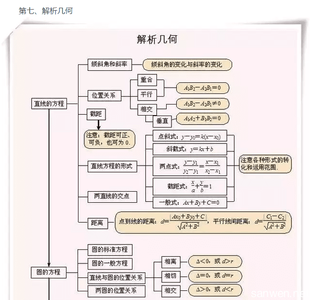
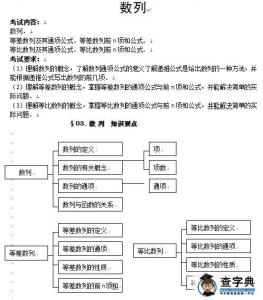
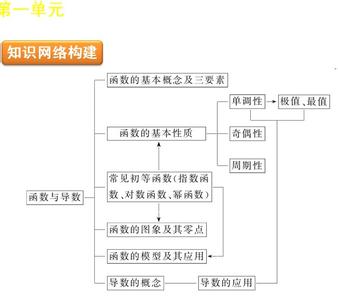
一、导数的概念
典型例题1:
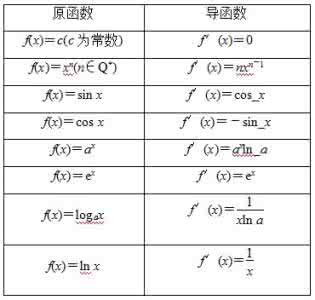
二、基本初等函数的导数公式
典型例题2:
三、导数的运算法则
4、复合函数的导数
复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为yx′=yu′·ux′,即y对x的导数等于y对u的导数与u对x的导数的乘积.
典型例题3:
四、函数求导的原则
对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.
曲线y=f(x)“在点P(x0,y0)处的切线”与“过点P(x0,y0)的切线”的区别与联系
(1)曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,切线斜率为k=f′(x0)的切线,是唯一的一条切线.
(2)曲线y=f(x)过点P(x0,y0)的切线,是指切线经过P点.点P可以是切点,也可以不是切点,而且这样的直线可能有多条.
典型例题4:
五、根据导数的定义,求函数y=f(x)在x=x0处导数的步骤
典型例题5:
求导时应注意:
(1)求导之前利用代数或三角恒等变换对函数进行化简可减少运算量.
(2)对于商式的函数若在求导之前变形,则可以避免使用商的导数法则,减少失误.
导数的几何意义是切点处切线的斜率,应用时主要体现在以下几个方面:
(1)已知切点A(x0,f(x0))求斜率k,即求该点处的导数值:k=f′(x0);
(2)已知斜率k,求切点A(x1,f(x1)),即解方程f′(x1)=k;
【作者:吴国平】
 爱华网
爱华网