6.3 正割法
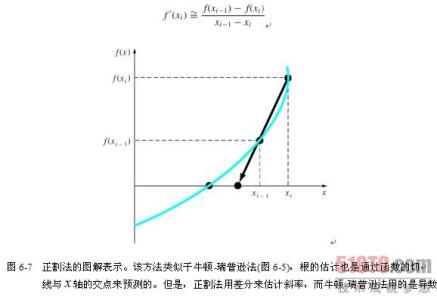
牛顿-瑞普逊法在实现时有一个潜在的问题:导数的计算。尽管对于多项式和其他很多函数来讲这并不是问题,但是一些函数的求导异常困难或者不方便求导。对于这种情况,导数通常使用后向有限差商来逼近,如图6-7所示。
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=397 alt="" src="http://pic.aIhUaU.com/201602/15/172251152.jpg" width=578 border=0>[/TD][/TR]
[TR][/TR]将这个近似表达式代入式(6.6)中,得如下迭代公式:
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=72 alt="" src="http://pic.aIhUaU.com/201602/15/172316727.jpg" width=265 border=0>[/TD][/TR]
[TR][/TR]
式(6.7)即为正割法的公式。这个方法需要两个 的初始估计值,然而它不属于划界法,因为f(x)不需要在这两个初始估计值之间改变符号。
例6.6 正割法
[TR]
[TD][I]498)this.width=498;' onmousewheel = 'javascript:return big(this)' height=495 alt="" src="http://pic.aIhUaU.com/201602/15/172502453.jpg" width=588 border=0>[/TD][/TR]
[TR][/TR]
 爱华网
爱华网



