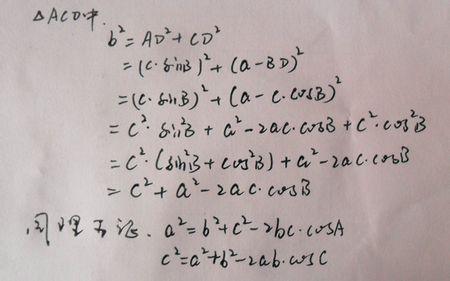中文名称
正弦定理
外文名称
sine theorem
应用学科
数学
适用领域范围
几何
目录展开B 为本词条添加义项名? 正弦定理是三角学中的一个定理。它指出了三角形三边、三个内角以及外接圆半径之间的关系。基本信息中文名称
正弦定理
外文名称
sine theorem
应用学科
数学
适用领域范围
几何
目录展开1 定理内容2 证明3 定理变形4 应用领域5 定理的意义6 扩展 1 定理内容正弦定理
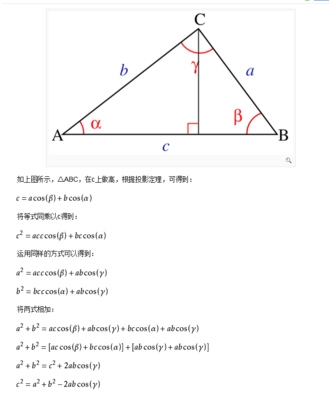
在△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R。
则有
正弦定理
即,在一个三角形中,各边和它所对角的正弦之比相等,该比值等于该三角形外接圆的直径长度。
2 证明步骤1.
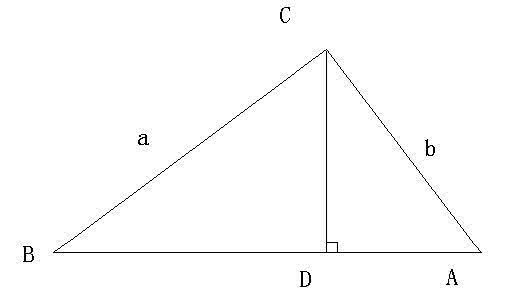
在锐角△ABC中,设BC=a,AC=b,AB=c。作CH⊥AB垂足为点H
CH=a·sinB
CH=b·sinA
∴a·sinB=b·sinA
得到
a/sinA=b/sinB
同理,在△ABC中,
b/sinB=c/sinC
步骤2.
证明a/sinA=b/sinB=c/sinC=2R:
如图,任意三角形ABC,作ABC的外接圆O.
作直径BD交⊙O于D.
连接DA.
因为直径所对的圆周角是直角,所以∠DAB=90度
因为同弧所对的圆周角相等,所以∠D等于∠C.
所以c/sinC=c/sinD=BD=2R
类似可证其余两个等式。
3 定理变形a:b:c=sinA:sinB:sinC
s=1/2a x b x sinC=1/2a x c x sinB=1/2b x c x sinA
a:sinA=b:sinB=c:sinC=(a+b+c):(sinA+sinB+sinC)
4 应用领域在解三角形中,有以下的应用领域:
(1)已知三角形的两角与一边,解三角形
(2)已知三角形的两边和其中一边所对的角,解三角形
(3)运用a:b:c=sinA:sinB:sinC解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
5 定理的意义正弦定理指出了任意三角形中三条边与对应角的正弦值之间的一个关系式。由正弦定理在区间上的单调性可知,正弦定理非常好地描述了任意三角形中边与角的一种数量关系。
一般地,把三角形的三个角A、B、C和它们的对边a、b、c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。
6 扩展一.三角形面积公式:
1.海伦公式:
设P=1/2(a+b+c)
S△=根号下P(P-a)(P-b)(P-c)
解释:假设有一个三角形,边长分别为a、b、c,三角形的面积S可由以下公式求得:
S=√[p(p-a)(p-b)(p-c)]
而公式里的p为半周长:
p=(a+b+c)/2
2. S△ABC=ab·sinC/2=bc·sinA/2=ac·sinB/2=abc/(4R)[R为外接圆半径]
3.S△ABC=ah/2
二. 正弦定理的变形公式
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
(条件同上)
在一个三角形中,各边与其所对角的正弦的比相等,且该比值都等于该三角形外接圆的直径已知三角形是确定的,利用正弦定理解三角形时,其解似的唯一的;已知三角形的两边和其中一边的对角,由于该三角形具有不稳定性,所以其解不确定,可结合平面几何作图的方法及“大边对大角,大角对大边”定理和三角形内角和定理去考虑解决问题
(3)相关结论:
a/sinA=b/sinB=c/sinC=a+b/sinA+sinB=a+b+c/sinA+sinB+sinC
 爱华网
爱华网