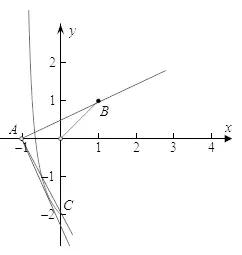
一次函数数形结合数形结合解决函数零点问题，最简单！-爱华网

小数老师说

今天又是一道函数零点的题目，通过这种题目出现的概率，大家也可以看到，这真是高考的热点啊！所以，同学们学与不学，自己选择吧！

通过上面的图像，我们可以找到4个临界的点，分别求出对应的m值，其范围就能确定了！

选择答案A。

注：在第一个临界范围的时候，一次函数与双曲线函数是相切的，利用导数的几何定义或者联立方程，令判别式等于0均可以。

3.读写结合的理论依据数形结合的理论依据

3.读写结合的理论依据(丁有宽教育思想）在总结读写结合四条基础经验的基础上，我进一步概括了读写结合符合六条基本理论，并把它渗透和运用到读写结合的教材教法和学法中去。一、读写结合符合学习迁移原理我认真地探索读与读、读与写的迁

Noip2009靶形数独解题报告（位运算版）语言：C++作者：副博主实现方法：搜索技巧：位运算此题以及类似题目（如八皇后），最明智的选择都是位运算实现。理由：思考：普通搜索时间都浪费到哪里了？答曰：1.查哪一位是空的，也就是没填；2.试探这一个空位可

一次函数是形如“y=kx+b(k为不为0的数）”，反映因变量y随着自变量x变化而变化的函数。是初中阶段研究的一种重点函数。在某一个变化过程中，设有两个变量x和y，如果可以写成y=f(x)，（即x经过某种运算得到y），即每一个x都有唯一一个y与之对应，那么

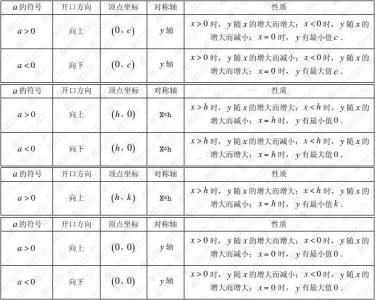
　　函数中，有一种多项式函数形如y=ax^2+bx+c（a，b，c是常数，a≠0），最高次数是2，这种函数，我们称之为二次函数。二次函数知识点颇多，初高中都会出现，在初中，刚刚出现在一次函数数形结合学习之后，因此，二次函知识点离不开数形结合思想。　　二次函数

一、绪论恩格斯说过：“数学是研究现实世界的量的关系与空间形式的科学”.数学中的两大研究对象“数”和“形”的矛盾统一是数学发展的内在因素.数形结合是贯穿于数学发展的一条主线，使数学在实践中的应用更加广泛和深远.一方面，借助