随机变量的数学期望 2009年考研数学辅导之随机变量及其分布-爱华网

2009年考研数学辅导之随机变量及其分布

额头

数学期望、泊松分布与足球赔率泊松分布的期望和方差

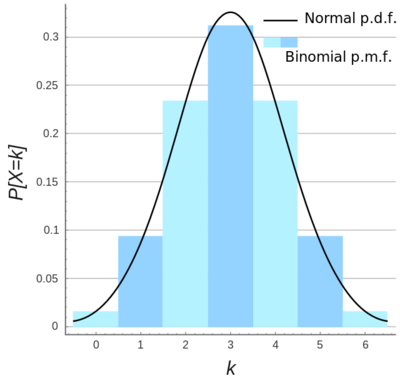
1.数学期望设离散随机变量的概率分布为P(=xi)=p(xi),(i=1,2,...),若其函数η=f(ξ),则随机变量η的数学期望定义为2.泊松分布

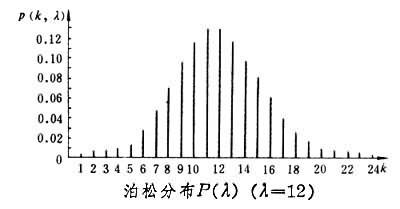
设随机变量　　，则再计算　　，故一、Poisson分布的概念Poisson分布更多地专用于研究单位时间、单位人群、单位空间内，某罕见事件发生次数的分布。如某种细菌在单位容积空气或水中出现的情况，某段时间特定人群中某种恶性肿瘤患者的分布或

期望基本解释：①对未来情况寄托希望或有所等待：期望能有成功的一天。又解，对未来的事物和人的前途有所希望和等待。eg.绝不辜负大家的期望。②又称“数学期望”、“均值”。概率论的基本概念。指随机变量ξ取值的加权平均数，其权数

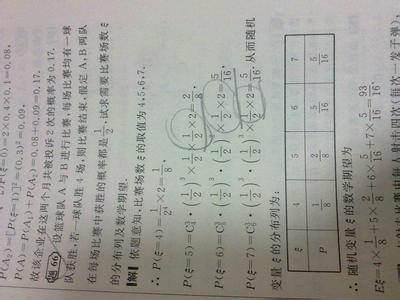
随机变量（random variable）表示随机现象（在一定条件下，并不总是出现相同结果的现象称为随机现象）中各种结果的实值函数（一切可能的样本点）。例如某一时间内公共汽车站等车乘客人数，电话交换台在一定时间内收到的呼叫次数等，都是随机变量的实

数学期望，早在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得100法郎的奖励。当比赛进行到第三局的时候，甲胜了两局，乙胜了一局，这时由于某