一道1985年高考解析几何题的两个优美解湖北省阳新县高级中学 邹生书#TRS_AUTOADD_1313566015061 {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1313566015061 P {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1313566015061 TD {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1313566015061 DIV {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1313566015061 LI {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}/**---JSON--{"":{"margin-top":"0","margin-bottom":"0"},"p":{"margin-top":"0","margin-bottom":"0"},"td":{"margin-top":"0","margin-bottom":"0"},"div":{"margin-top":"0","margin-bottom":"0"},"li":{"margin-top":"0","margin-bottom":"0"}}--**/DIV.MyFav_1313566016276 P.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1313566016276 LI.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1313566016276 DIV.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1313566016276 P.MsoFooter{FONT-SIZE: 9pt; MARGIN: 0cm 0cm 0pt; LAYOUT-GRID-MODE: char; FONT-FAMILY: "Times New Roman"}DIV.MyFav_1313566016276 LI.MsoFooter{FONT-SIZE: 9pt; MARGIN: 0cm 0cm 0pt; LAYOUT-GRID-MODE: char; FONT-FAMILY: "Times New Roman"}DIV.MyFav_1313566016276 DIV.MsoFooter{FONT-SIZE: 9pt; MARGIN: 0cm 0cm 0pt; LAYOUT-GRID-MODE: char; FONT-FAMILY: "Times New Roman"}DIV.MyFav_1313566016276 A:link{COLOR: blue; TEXT-DECORATION: underline}DIV.MyFav_1313566016276 SPAN.MsoHyperlink{COLOR: blue; TEXT-DECORATION: underline}DIV.MyFav_1313566016276 A:visited{COLOR: purple; TEXT-DECORATION: underline}DIV.MyFav_1313566016276 SPAN.MsoHyperlinkFollowed{COLOR: purple; TEXT-DECORATION: underline}DIV.MyFav_1313566016276 DIV.Section1{page: Section1}题目 已知椭圆,直线,是上一点,射线交椭圆于点,又点在上,且满足,当点在上移动时,求点的轨迹方程,并说明轨迹是什么曲线.
这是1985年高考的一道解析几何题,文[1]的两个解法较繁运算量较大,本文笔者运用新课标教材知识内容从极坐标和向量两个角度切入给出两个优美解与大家分享.
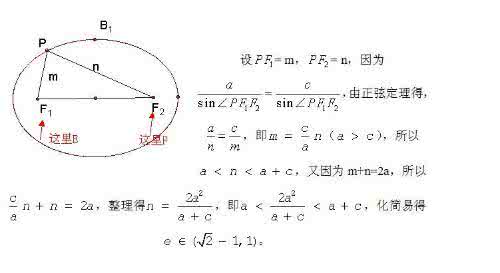
优美解1(极坐标法)如图,依题意设三点的极坐标分别为.因点在椭圆上, 故有,所以①.
又点在直线上,所以有,即②.又由得③ .由①②③得,即,所以,化为直角坐标方程得.又点不能是坐标原点,所以不同时为零,故点的轨迹方程是(),即,其轨迹是中心为焦点在直线上的椭圆(坐标原点除外).
优美解2(向量方法)依题意设,设,则,因点在直线上,故有即①.又点在椭圆上,所以有即②. 又由得即③.由①②③得,即,下同法1略.
问题是数学的心脏,问题解决是数学的核心和目标,简单优美是数学的更高追求,根据问题特点灵活选择恰当的方法使问题得以轻松解决,可从中可体验创造美、发现美、欣赏美的愉悦和成功.
参考文献:
乔家瑞..特级教师点拔高考数学卷[M]..北京学苑出版社,1998年8月第二版.
爱华网本文地址 » http://www.aihuau.com/a/405351/35411019665.html

 爱华网
爱华网