实际气体状态方程
state for actualgases,equation of
描述实际气体状态变化规律的方程。实际气体的分子有内在结构,两分子相距较近时为斥力且随距离缩短急剧增大,相距较远时为引力随距离加大逐渐减小。实际气体与理想气体微观模型的差异,导致状态方程不同。
1873年范德瓦耳斯假设气体分子是相互吸引的刚球,吸引力范围大于刚球半径。因分子是刚球而不是质点,分子活动范围即气体体积小于容器容积 V ,气体体积应修正为(V-b),b是反映分子大小的修正量,可由实验确定。又因分子间存在吸引力,当分子在容器内部时,四周分子对称分布合力为零;但当分子与器壁距离小于吸引力作用范围时,将受到垂直于器壁指向气体内部的合力,使分子撞击器壁时动量的垂直分量减小,即器壁所受实际压强比
小,为,称为气体分子施予单位面积器壁的冲量的平均值。分子碰壁一次施予的冲量(即分子动量的改变)的减少量与分子所受吸引力成正比,吸引力又与单位体积分子数成正比,同时,碰壁的分子数也与单位体积分子数成正比。因此,Δp应与体积的二次方成反比,为,a是常量可由实验确定。于是,1摩尔范德瓦耳斯气体的状态方程为:
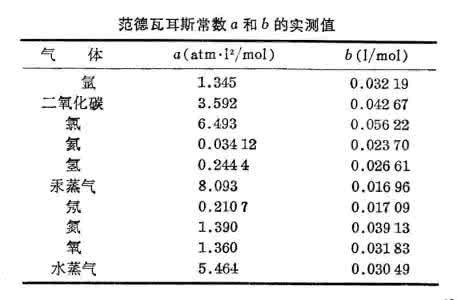
范氏方程较好地描绘高温下实际气体的状态变化关系,揭示出相变临界温度的存在,推广后还可近似应用于液体。它是许多近似状态方程中最简单和使用最方便的一个。
卡末林-昂内斯提出了一个按体积负幂次展开的级数形式的气体物态方程
式中A,B,C,…都是温度的函数,并与气体性质有关,分别称为第一、第二、第三…位力系数。这是实际气体状态方程最完全的形式。
实际工作中常采用各种经验或半经验的状态方程,它们相当准确,但往往只适用于某种特定气体或蒸气,只限于特定的比较狭小的压强和温度范围。以上就是网友分享的关于"实际气体状态方程"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网