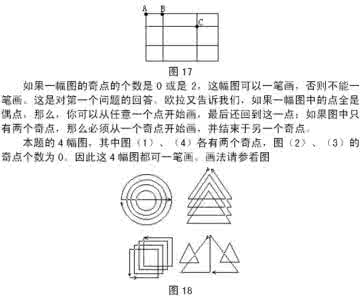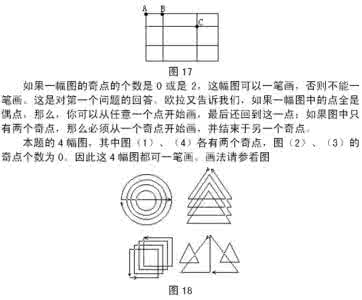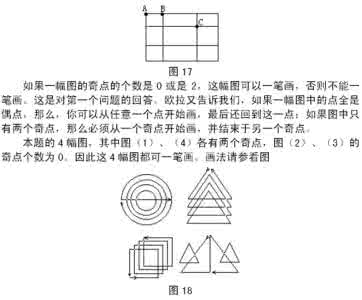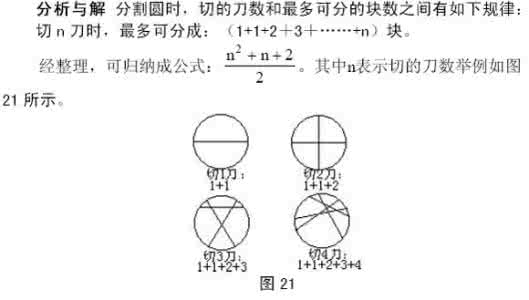
六年级奥数之趣味数学13
37.五个好朋友
A、B、C、D、E 五个学生是同班的好朋友,其中有四人做课代表工作,这四科是语文、数学、地理、历史。另一个人是中队长。
请你根据下列条件,判断出这五位同学各做什么工作。
(1)语文课代表不是C,也不是D;(2)历史课代表不是D,也不是A;(3)C和E住在同一楼里,中队长和他们是邻居;(4)C问数学课代表问题时,B也在一旁听着;(5)A、C、地理课代表、语文课代表常在一起讨论问题;(6)D、E常到数学课代表家去玩,而中队长去的次数不多。
分析与解 A是数学课代表,B是中队长,C是历史课代表,D是地理课代表,E是语文课代表。
题中(1)、(2)是直接条件,而(3)~(6)就不像(1)、(2)那
38.过队日
六(1)中队共43名队员,他们到龙潭游乐园过中队日。中队长宣布,大家只能参加“激流勇进”、“观览车”和“单轨火车”三种游乐活动。活动结束时,中队长说:“根据今天参加游乐活动的情况我编了一道数学题:全中队至少有多少人参加的活动完全相同?”
你能替六(1)中队的同学找到正确答案吗?
分析与解 全中队至少有7人参加的活动相同。
这是一道根据实际活动编得很有趣的数学题。解答这道题首先要弄明白同学们参加游乐活动共有几种可能情况。我们把各种情况分别列出如下:(1)只参加“激流勇进”;(2)只参加“观览车”;(3)只参加“单轨火车”;(4)既参加“激流勇进”,又参加“观览车”;(5)既参加“激流勇进”,又参加“单轨火车”;(6)既参加“观览车”,又参加“单轨火车”;(7)三种活动都参加。
由于可能的情况共有7种,去游乐场的有43名少先队员, 43÷7=6……1(人),即如果每种可能的情况有6名队员参加的话,那么还余1名队员,不管这1名队员参加活动属于哪种“情况”,则至少有7人参加的活动相同。
39.放硬币游戏
参加人:2人,也可以有裁判1人。
用具:一张纸(方形、圆形都可以),1分硬币若干枚。
游戏规则:①2人轮流把硬币放在纸上,每人每次只放一枚;②放在桌上的硬币不能重叠;③最后在纸上无处可放者为负。
同学们,要想在这个小游戏中取胜,只需应用几何中一个很简单的原理。你知道怎样放才能保证在游戏中稳操胜券吗?
分析与解 这个游戏对参加的两个人来说是不平等的,如果知道了游戏的奥妙,那么先放硬币的一方会稳操胜券。
游戏的奥妙是利用平面几何中的中心对称原理。先放者,首先抢占“对称中心”,即纸的中心。然后,不论对方把硬币放在什么位置,你每次都根据中心对称原理,把硬币放到对方硬币的对称位置上。这样,只要对方有地方放,你就必定有放的地方,直到你占满最后一处空白,逼得对方无处可放,你就获胜了。
 爱华网
爱华网