第十章 质点系动力学基础
习题解析
10-1质点系的内力是否影响质点系的动量改变和质心运动?是否影响质点系的动量矩改变?是否影响质点系的动能改变?
答:质点系的内力总是成对地出现的,内力的矢量和等于零,或者说内力的冲量和等于零。所以质点系的内力不影响质点系的动量改变和质心运动。
质点系的内力成对出现,内力的力矩和为零,即内力的主矩为零。所以质点系的内力不影响质点系的动量矩改变。
如果质点系内各质点之间的距离可变, 作用于两个质点之间的内力虽成对出现且等值、反向、共线,但内力作功的和并不等于零。例如炸弹爆炸、内燃机汽缸活塞工作等都是内力作功。在此情况下,质点系的内力影响质点系的动能改变。
10-2 人站在初始静止的小车上,小车可沿水平直线轨道运动,不计摩擦,人由一端慢慢走向另一端和快跑到另一端,车后退的距离是否相等?为什么?
答:由于不计摩擦,系统在水平方向所受外力为0。按照质心运动守恒定理,不论人由一端慢慢走向另一端还是快跑到另一端,系统质心总是不变的,所以车后退的距离是相等的。 10-3 动量和动量矩有何异同?
答:质点的动量是质量与速度的乘积。质点系的动量为质点动量的矢量和。
质点的动量矩是定点O到质点的矢径与质点动量的叉积。质点系的动量矩为质点的动量矩的矢量和。
10-4 质点系的质量为m,质心速度为vC,各质点质量为mi,速度为vi,使用以下公式计算质点系对z轴的动量矩是否正确?为什么?
?Mz(mivi)?Mz(mvC)
i?1n
答:不正确。
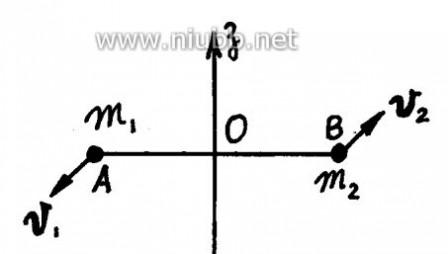
以图10-3所示为例,设AB杆质量不计,二端固定的质点m1、m2质量均为m/2,AB杆绕z轴转动,已知OA?OB?r,v1?v2?v , 则
图10-3
?Mz(mivi)?m1v1r?m2v2r?mvr
i?1n
Mz(mvC)?0
所以使用?Mz(mivi)?Mz(mvC)公式计算质点系对z轴的动量矩是不正确的。
i?1n
10-5 在什么条件下质点系的动量矩守恒?
答:当作用在质点系的外力对某固定点之矩的矢量和为零,质点系对该点的动量矩保持不变,即质点系对固定点的动量矩守恒。
若作用于质点系的外力对某轴之矩的代数和为零,质点系对该轴的动量矩保持不变,即质点系对该轴的动量矩守恒。
10-6 如图10-4所示,均质圆盘质量为m,半径为r,角速度为ω,计算其动能。
图10-4 题10-6图
解 a) 均质圆盘绕质心O转动,动能为
1mr2?22T?JO?? 24
b) 均质圆盘绕边缘上O点转动,动能为
11mr232T?JO??(?mr2)?2?mr2?2 2224
c) 均质圆盘作纯滚动,即作平面运动。作平面运动的刚体的运动可分解为随质心O的平动及绕质心O的转动。质心速度为vC?vO??r,绕质心O转动的角速度为ω,则圆盘的动能为
T?1213mvC?JC?2 ?mr2?2 224
10-7质点的惯性力是否作用在质点上?什么叫达朗贝尔原理?
答:质点的运动状态改变时,由于质点的惯性,质点将给予施力体一个反作用力,这个反作用力称惯性力。质点的惯性力是作用在施力物体上的,它并不作用在质点上。
质点的达朗贝尔原理:在质点运动的任一瞬时,作用于质点的主动力、约束力和质点的惯性力构成一组平衡力系。
质点系的达朗贝尔原理:在质点系运动的每一瞬时, 作用在质点系上的所有外力和所有质点的惯性力在形式上组成一平衡力系。
10-8 跳伞运动员质量为70kg, 从停留在空中的直升飞机跳出(初速度为零),落下100m后降落伞打开,开伞前的空气阻力不计,开伞后的空气阻力为常数,经5秒后跳伞者的速度减为4m/s,求空气阻力的大小。
解 如图10-5所示,分二个阶段:
1)运动员从停留在空中的直升飞机A点跳出,自由下落100m到O点
2)O点开伞,经5秒后跳伞者到达B点
图10-5
第一阶段:
22vO?vA?2gh1
其中vA?0,h1?100m,故vO?
第二阶段: 2gh1?44.3m/s
mg?FO?ma 其中加速度a?vB?vO4?44.3?m/s2??8.06m/s2,空气阻力的大小 t5
FO?mg?ma?[70?9.8?70?(?8.06)]m/s2?1250N
10-9 质量为3kg, 倾角为30°的斜面C可在光滑水平轨道上运动,物块A的质量mA?6kg,轮O的质量不计。当A在斜面无初速地下滑过0.4m时,斜面在水平轨道上滑过的距离为0.2m,求物体B的质量。
图10-6 题10-9图
解 如图10-6所示,作用在质点系上的外力在某水平轴x上的投影为零, 系统质心初速度为0。由质心运动守恒定理可知,当物块A在斜面上滑动时,系统质心在水平轴x上的坐标不变。即
mA?xA?mB?xB?mC?xC?0
?xA?sC?sAcos300,?xB??xC?sC,所以物体B的质量
mA?xA?mC?xC6?(0.1?0.4?cos300)?3?0.1mB????kg?11.78kg B10-10 重物A和B的质量分别为mA?10kg,mB?15kg,通过质量不计的绳索缠绕在半径为r1和r2的塔轮上,其中r1?0.12m,r2?0.18m,塔轮的质量不计,如图10-7所示。系统在重力作用下运动,求塔轮的角加速度。
图10-7 题10-10图
解 由于mAr1<mBr2,物体B下降,物体A上升。考虑物体A、B、圆盘及绳索组成的系统,对垂直于圆盘平面的转轴O应用动量矩定理。设v为物体A、B的瞬时速度,ω为圆盘的角速度,有以下关系:
vA??r1,vB??r2
计算系统对O轴的动量矩
H0?mAvAr1?mBvBr2?(mAr12?mBr22)?
系统外力对O轴的力矩为
Mo?mBgr2?mAgr1
根据动量矩定理
dHo?Mo dt
得 (mAr12?mBr22)??(mBr2?mAr1)g
求得塔轮的角加速度
??mBr2?mAr115?0.18?10?0.12g??9.8rad/s2?23.3rad/s2 2222mAr1?mBr210?0.12?15?0.18
10-11 如图10-8所示,质量为100kg,半径为1m的均质圆轮以转速n=135r/min绕轴O转动,设有一常力F作用于闸杆端点,由于摩擦使圆轮停止转动。已知F=300N,闸杆与圆轮间的摩擦因数f=0.25,求使圆轮停止所需的时间。
图10-8 题10-11图
解 由杠杆定理可知,作用在均质圆轮上的正压力
FN?F?(1.2?1.8)?1.2?750N
圆盘的受力如图10-9所示,只有摩擦力Ff对O轴的力矩不为零,根据刚体绕定轴转动运动微分方程,可得
Jo???Ffr 式中Jo?121mr??100?12kg?m2?50kg?m2,摩擦力Ff?f?FN?187.5kN,故22
圆轮角加速度
图10-9
???Ffr/Jo??3.75rad/s2
设使圆轮停止所需的时间为t,开始制动时圆盘的角速度?o?2?n,角加速度定义60???t??0
t0??2?n,结合上式得到 t
2?n2?3.14?135t???s?3.77s 6060?(?3.75)
10-12 如图10-10所示物块自倾角为?斜面上A点无初速下滑,滑行L1至水平面,在水平面滑行L2至B点停止。设斜面和水平面与物块的滑动摩擦因数相同,已知?=25°,L1=0.15m,L2=0.18m,求物块与斜面的动摩擦因数。
图10-10 题10-12图
解 物块在斜面阶段滑动摩擦力
F1?FN1f?mgcos?f
物块在水平面阶段滑动摩擦力
F2?FN2f?mgf
物块从A到B摩擦力所作的功
Wf??mgf(L1cos??L2)
重力所作的功式
Wg?mgL1sin?
代入质点动能定理的积分形式:
1212mv?mv?Wf?Wg 2B2A
得到物块与斜面的动摩擦因数
L1sin?0.15?sin250f???0.2 L1cos?L20.15?cos250?0.18
10-13 物块C的质量为3m,上有一半径为r的半圆槽,放在光滑水平面上,如图10-11所示。质量为m的光滑小球可在槽内运动,初始时系统静止,小球在A点,求当小球运动到B点时物块C的速度。
图10-11 题10-13图
解 (1)考虑物体C和光滑小球M构成的系统,受到的外力有物体C和光滑小球M的重力,地面对物体C的约束力FN,所有外力都沿y轴方向,在x轴上受外力为零,根据动量定理,系统在x轴方向上动量守恒。
初始时系统静止,动量p0x?0,所以任一时刻px?0。设光滑小球M相对半圆槽的速度为vr,物体C向右运动的速度为vC,则光滑小球M的绝对速度为
vM?vC?vr
系统的动量在x轴上的投影
px?mCvC?mMvM?3mvC?m(vC?vr)
根据上述讨论,px?0,整理上式得到
vr?4vC (a)
(2) 小球从A点运动到B点过程中,只有重力作功,大小为
Wg?mMgr 代入质点系动能定理?21122(e)(i),得到: miviB??miviA??WAB??WABi?12i?12
112?3m?vC?m(vC?vr)2?mgr 222
2即 3vC?(vC?vr)2?2gr (b)
联立(a)、(b)二式,得到当小球运动到B点时物块C的速度vC?gr。 6
10-14 物块的质量为m,在半径为r的光滑半圆柱顶点A以初速度v0滑下,当物块到达如图10-12所示位置时,求物块的速度和对圆柱的压力,并求当角θ为何值时物块离开圆柱面。
图10-12 题10-14图
解 (1)物块从A点运动到B点过程中,只有重力作功,大小为
Wg?mgr(1?cos?) 代入质点动能定理1212mv?mv?Wg,得到物块的速度: 2B2A
2vB?v0?2gr(1?cos?)
(2)当物块到达图10-12所示位置时,物块受到重力mBg、圆柱压力FN,代入牛顿第二定律得:
2vBmB?mBgcos??FN r
所以物块对圆柱的压力
2vBm2??FN?mBgcos??mB?mgcos??[v0?2gr(1?cos?)] FNrr
(3)当物块离开圆柱面时:
FN?0,即 mgcos??m2[v0?2gr(1?cos?)]?0 r
22v0)时,物块离开圆柱面。 解得当角???33gr
10-15 如图10-13所示,小球质量为m,用长为L的细绳系于O点,以匀角速度ω绕铅垂线作圆周运动,绳与铅垂线成?角,求绳的拉力。
图10-13 题10-15图
解 如图10-13所示,小球受到重力mg、绳的拉力FT作用,小球的向心加速度为v2
??2Lsin?,代入牛顿第二定律得: Lsin?
m?2Lsin??FTsin?
所以绳的拉力大小为FT?m?2L。
 爱华网
爱华网