线面的位置关系
二. 知识总结:
直线与平面的位置关系
1. 直线在平面内——直线与平面有无数个公共点
2. 直线在平面外
(1)直线与平面相交——直线与平面有且仅有一个公共点
① 直线与平面直交(垂直)
② 直线与平面斜交(不垂直)
(2)直线与平面平行——直线与平面没有公共点
(一)直线与平面平行的判定和性质
1. 判定依据
(1)线面平行的定义
(2)线面平行的判定定理(又称线线平行则线面平行)
(3)面面平行的性质:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面
2. 判定方法
(1)证明这直线与这平面没有公共点
(2)证明这直线与这平面内的某条直线平行
(3)证明这直线所在平面与这平面平行
(4)证明这直线上有在平面同旁的两点到这个平面距离相等
3. 性质
(二)直线和平面垂直的判定和性质
1. 知识提要
(1)直线和平面垂直的定义
如果一条直线和平面内的任何一条直线都垂直,就称这条直线和这个平面互相垂直。
(2)直线和平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
(3)两两平面垂直的性质定理
如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
2. 方法提要:判定直线垂直平面的方法
(1)证明这直线与平面内两条相交直线都垂直
(2)证明这直线与平面的一条垂线平行
(3)证明这直线所在平面垂直该平面,并且这直线垂直于两平面的交线
(4)证明这直线垂直于另一个平面,而这个平面与已知平面互相平行
(5)证明直线是这平面的两个相交垂面的交线
【典型例题】
[例1] 已知:正方形ABCD与正方形ADEF所在平面相交,M、N分别是BD、AE内的动点,且BM=AN,求证:MN//平面CED。
证明:连结AM并延长交CD于G,连结GE
由AB//CD
[例2] 设S是平行四边形ABCD所在平面外一点,P、Q、R分别是SC、SB、SD上的点,且,求证:SA//平面PQR。
证:如图,设,则O为AC的中点,连结SO
设,由
取SC中点M,连结OM、KP
由
[例3] 正三棱柱中,。D、F分别为CC1,A1B中点
(1)证明:DF//平面ABC;
(2)证明:AF⊥BD;
(3)求平面A1BD与ABC所成的锐二面角
(1)证明:取AB中点M,连FM、CM
(2)证明:
(3)法1:
法2:延长AC交A1D延长线于G,连BG,由CG=AC=BC
又AA1⊥面ABC为所求二面角平面角
[例4] 如图,在正三棱柱中,,求证:,。
证法1:如图,延长B1C1到,使,连结,则
在中,由
同理
证法2:(利用三垂线Th及其逆Th)
如图,取AB的中点为D,A1B1的中点为D1,则BD1//A1D
同理面A1B1BA
,同理A1C⊥BC1
[例5] 如图,AB是圆O的直径,PA垂直于圆O所在平面,且PA=AB,C是圆周上一点(异于A、B),E是PB的中点,F是PC上的点,且AF⊥PC,求证:PB平面AEF。
证:
[例6] 已知矩形ABCD,过A作SA⊥平面AC,作AE⊥SB交SB于E,过E作EF⊥SC于F。
(1)求证:AF⊥SC;
(2)若平面AEF交SD于G,求证:AG⊥SD。
证明:(1)由已知,SA⊥平面AC
(2)证明:
[例7] 斜三棱柱中,底面是边长为的正三角形,一条侧棱AA1与底面相邻两边AB、AC都成角,求异面直线与BC的距离。
解:由在面ABC上的射影H在的平分线上
连AH延长交BC于D,则AD是的平分线
作DE⊥AA1于E,则DE即异面直线AA1与 BC的公垂线段
又由
∴
∴ 在中,
即与BC的距离为
[例8] 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2,求点B到平面EFG距离。
解:如图,连结EG、FG、EF、BD、AC
设,
到面EFG的距离与点B到面EFG距离相等点O到面EFG的距离与B到面EFG的距离相等
由
由GC=2,
,则
另法(体积变换)
解法2:设点B到面EFG的距离为,则为三棱锥B-EFG的高,由三棱锥与三棱锥为同一四面体,故它们体积相等,即:
而
故
所以,点B到平面EFG的距离为
小结:点到面的距离有直接和间接两类方法,直接法即作出点面垂线段并求它的长;而间接法是把点面距离看成一个几何体的高,再利用体积变换方法求出这个高的值,通常情况下,由于间接法无需确定垂足的位置,因此较为简便。
[例9] 如图,四棱锥中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为重心,则PG与底面所成角为( )
A. B. C. D.
解:如图,由G为的重心,则为所求,,,,则,即,选B。
[例10] 已知异面直线与所成的角为,P为空间一定点,则过点P且与所成的角都是的直线有且仅有( )
A. 1条 B. 2条 C. 3条 D. 4条
解:把直线分别平移至经过点P,即:过点P分别作直线,,如果,则取;如果,则取。这时,与相交于点P所成的两组对顶角分别等于和,记与所确定的平面为,那么,在平面内,过点P不存在与都成的直线。
过点P且与都成角的直线,必在面外且在内的射影必然平分所成的对顶角,这样的直线有且仅有2条,它们关于对称,所以,过点P与都成角的直线有且仅有2条,故选B。
若不变,将改为则答案A;若不变,将改为度,则答案为C;若不变,将改为,则答案为D。
[例11] 如图,斜三棱柱的底面为一等腰直角三角形,直角边AB=AC=,侧棱与底面成,,求与底面所成的角。
解:由AC⊥AB,AC⊥面面面ABC,故在底面ABC上的射影即AB所在直线。
过作交AB延长线于点O,连CO,则分别是与底面所成的角
∴ ,令,则,在中,
在中,由,
即
(舍)与底面所成角为
注:线面角取值范围,关键找到直线在面上的射影,一般先找斜足,再找线上非斜足一点P在该平面内射影,连转化为平面角。
[例12] 三棱锥中底面ABC为边长为的正三角形,PA、PB与底面均成角,PC与底面成角,求其体积。
解:设M是AB中点,由PA与PB与底面均成角,故PA=PB
面PCM面ABC⊥PCM
作PH⊥CM于H,则PH⊥底面ABC
则,,设,则
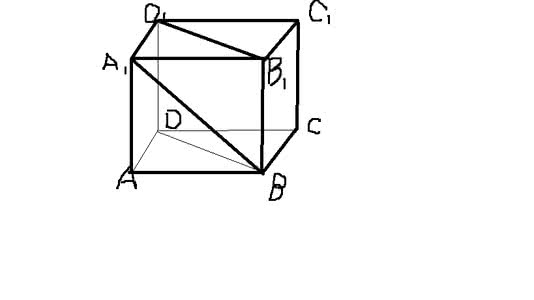
又
∴
∴ 或
当时,H=M ,
当时,,PH=,V=
【模拟试题】
一. 选择题
1. 两条直线与平面所成的角相等,则的位置关系( )
A. 平行 B. 相交 C. 异面 D. 以上都有可能
2. 空间两条直线平行的充分条件是( )
A. 平行于同一平面 B. 垂直于同一条直线
C. 与同一平面所成的角相等 D. 分别垂直于两个平行平面
3. 如果AP、BP、CP两两垂直,则P在平面ABC内的射影一定是△ABC的( )
A. 垂心 B. 内心 C. 外心 D. 重心
4. 下列命题中不正确命题的个数是( )
(1)如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直;
(2)过平面外一点,可作无数条直线和这个平面垂直;
(3)过一点有且仅有一个平面和一条定直线垂直;
(4)若异面,过一定可作一个平面与b垂直。
(5)若异面,过不在上的点M,一定可以作一个平面与a、b都垂直
A. 1个 B. 2个 C. 3个 D. 4个
5. 若直线与平面所成的角为,直线在平面内,且与直线异面,则直线与直线所成的角的取值范围是( )
A. B. C. D.
6. 在正方体ABCD—A1B1C1D1中,M、N分别是棱AA1、AB上的点,且∠NMC1=90°,则∠NMB1的大小是( )
A. 大于90° B. 小于90° C. 90° D. 不能确定
7. 已知PA、PB、PC是从点P出发的三条射线,每两条射线的夹角均为60°,则直线PC与平面PAB所成角的余弦值为( )
A. B. C. D.
8. 已知正方体ABCD—A1B1C1D1中,E、F分别是AA1、BB1的中点,则EF与对角面ACC1A1所成角为( )
A. 30° B. 45° C. 60° D. 150°
9. 设a、b是两条异面直线,在下列命题中,正确的是( )
A. 有且仅有一条直线与a、b都垂直;
B. 有一个平面与a、b都垂直;
C. 过直线有且仅有一个平面与b平行;
D. 过空间任意一点必可作一条直线与a、b都相交。
10. 已知直线不在平面内,那么下列命题正确的个数为( )
(1)若不平行于,则不平行于内的任何直线;
(2)若平行于,则平行于内的所有直线;
(3)若平行于,则与垂直的任何直线与平面垂直;
(4)若垂直于内无数条直线,则必有⊥。
A. 0 B. 1 C. 2 D. 3
11. 在正方形ABCD中,E、F分别是BC、CD的中点,D是EF的中点,现沿AE、AF和EF把这个正方形折成一个四面体,使得B、C、D三点重合,重合后变为G点,则四面体A—EFG中必有( )
A. AG⊥平面EFG B. AD⊥平面EFG
C. GF⊥平面AEF D. GD⊥平面AEF
12. 在Rt△ABC中,∠B=90°,∠C=30°,D是BC边的中点,AC=2,DE⊥平面ABC且DE=1,则点E到AC边的距离为( )
A. B. C. D.
二. 填空题
13. 已知P是△ABC所在平面外一点,O是P在平面ABC内的射影。若PA=PB=PC,则点O是△ABC的 。
14. 已知直线是平面的斜线,,与b所成的角为60°,b与在内的射影所成的角为45°,则与所成的角为 。
15. 在△ABC中,AB=AC=5,BC=6,且PA⊥平面ABC,则点P到BC的距离为 。
16. 已知A、B、C、D四点不共面,则与这四个点距离都相等的平面有 个。
17. 长方体ABCD—A1B1C1D1中,棱AA1=5,AB=12,则直线B1C1到平面A1BCD1的距离是 。
18. 直角三角形的斜边AB在平面内,AC和BC与所成角分别为30°,45°,CD是斜边AB上的高,则CD与所成的角为 。
19. 已知正方形ABCD—A1B1C1D1棱长为,E是CC1中点,则BE与平面B1BD所成的角的余弦值是 。
20. Rt△ABC,∠ACB=90°,CD⊥,梯形ACDE,AC//DE,BE⊥AE,且AC=2,DE=1,则异面直线AE和BC的距离是 。
【试题答案】
一. 选择题
1. D
2. D
提示:利用线面垂直的判定定理和性质定理。
3. A
4. D
提示:从(1)—(5)命题中,只有(3)为真命题,其余均为假命题。
5. B
提示:利用最小角定理和直线与平面所成角的范围为可得。
6. C
提示:利用三垂线定理的逆定理。
7. D
提示:如答图1,作CO⊥面PAB于O,连结PO
由∠CPA=∠CPB=60°,则PO为∠APB的平分线,∠APO=30°,∠CPO为所求线面角,由例4给出的关系式,有
图1
8. A
提示:如答图2,作FG//BD交AC于G,由BD⊥面ACC1A1,则FG⊥面ACC1A1,连结GE,则∠FEG为EF与对角面ACC1A1所成的角。设正方体棱长为,则,,在Rt△FGE中,,故∠FEG=30°,选择A。
图2
9. C
提示:在上任取一点P,过P作,设与所确定的平面为,由,,则,可以证明这样的平面是惟一的。事实上,假设过有平面满足,则根据例2的结论,直线b平行于与的交线,即,这与异面矛盾。
10. B
提示:只有(1)是正确的。由不平行于,又不在内,则与相交,因此不平行于内的任何直线。
11. A
提示:AG⊥GF,且AG⊥GE,则AG⊥平面EFG。
12. D
提示:如答图3,作DF⊥AC于F,连结EF,则EF⊥AC,即EF为E到AC的距离。
由Rt△CFD~Rt△CBA,
图3
二.
13. 外心
提示:利用射影长Th
14. 45°
提示:利用例4已证的公式,设与所成的角为,则,因此
15.
提示:取BC中点M,连AM、PM,则由
,故PM为P到BC的距离
16. 7
提示:当平面的一侧有一点而另一侧有三点时,满足条件的平面有4个;当平面的两侧各有两个点时,满足条件的平面有3个。因此,与A、B、C、D四点距离都相等的平面共有4+3=7个。
17.
提示:作B1E⊥A1B于E,则B1E⊥平面A1BCD1,即B1E为直线B1C1与平面A1BCD1的距离。在
18. 60°
提示:如答图4,作CO⊥于O,∠CAO=30°,∠CBO=45°,∠CDO为CD与所成的角,设CO=x,则AC=2x,BC=,在Rt△ACB中
在Rt△COD中,,即∠CDO=60°
图4
19.
提示:如答图5,取F为AA1的中点,连结EF
设EF交OO1于M,则M为OO1中点,则∠EBM1为BE与平面B1BD所成的角
在Rt△EBM中,,则
图5
20.
提示:如答图6
故CE为异面直线BC与AE的公垂线段
由DE=1,AC=2,∠DCA=90°,∠CEA=90°,则
图6
 爱华网
爱华网