等差数列求和公式 等差数列求和公式-其他结论，等差数列求和公式

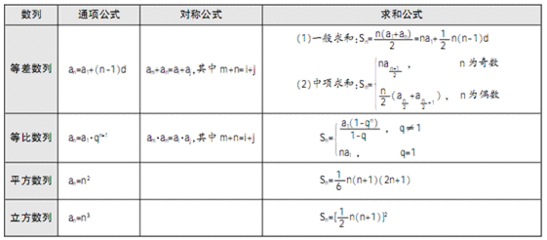
等差数列是常见数列的一种，如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，而这个常数叫做等差数列的公差，公差常用字母d表示。例如：1,3,5,7,9……（2n-1)。等差数列的通项公式为：an=a1+(n-1)d。前n项和公式为：Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。注意： 以上n均属于正整数。

等差数列求和_等差数列求和公式 -其他结论

首项：

末项：

通项公式：

项数：

公差：

如：数列1,3,5,7,……,97,99 公差就是d=3-1=2 将

推广到

，则为：

a1,a2,a3....an,n=奇数，Sn=（a（（n-1）/2)）*((n-1）/2)

等差数列求和_等差数列求和公式 -特殊性质

1.在数列

中,若

,则有:

①若

,则am+an=ap+aq.

②若m+n=2q,则am+an=2aq.

2.在等差数列中，若Sn为该数列的前n项和，S2n为该数列的前2n项和，S3n为该数列的前3n项和，则Sn，S2n-Sn，S3n-S2n也为等差数列。

等差数列求和_等差数列求和公式 -求和公式（字母）

设首项为

, 末项为

, 项数为

, 公差为

, 前

项和为

, 则有:

①

;

②

;

③

;

④

, 其中

..

当d≠0时，Sn是n的二次函数，（n，Sn）是二次函数

的图象上一群孤立的点。利用其几何意义可求前n项和Sn的最值。

注意：公式一二三事实上是等价的，在公式一中不必要求公差等于一。

求和推导

证明：由题意得：

Sn=a1+a2+a3+。。。+an①

Sn=an+a（n-1）+a（n-2）+。。。+a1②

①+②得：

2Sn=[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an](当n为偶数时)

Sn={[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an]}/2

Sn=n（A1+An）/2 (a1，an，可以用a1+（n-1）d这种形式表示可以发现括号里面的数都是一个定值，即A1+An）

等差数列求和_等差数列求和公式 -求和公式（文字）

【（首项+末项）*项数】÷2

首项*项数+【项数（项数-1）*公差】/2

{【首项*项数+（项数-1）*公差】项数}/2

爱华网本文地址 » http://www.aihuau.com/a/8103230103/23750.html