关键词:算法 简单带权图 最短路径 Dijkstra算法
中图分类号:TP311.13 文献标识码:A 文章编号:1007-9416(2016)11-0133-01
1 引言
最短路径问题:任给简单带权图及,求之间的最短路径及距离。最短路径问题的一个有效算法是Dijkstra算法。
2 Dijkstra算法
Dijkstra算法是一种标号法,每一个顶点有一个标号,标号分永久标号和临时标号两种,在顶点的标号记为。算法:
(1) 令,表示空,
。
(2) 对所有的且
令,
若,则令。
(3) 求。
令。
(4) 令,
若,则转(2)。
每一步有一个顶点获得永久标号,个顶点共要进行步。计算结束后,就是到的距离,而利用通过回溯可以得到到的最短路径。
3 Dijkstra算法的改进
i步骤(3)标号永久化的同时也将 中顶点的标号永久化;ii将和并入新一轮的。这样的增加量大于等于1,使得总计算步数小于等于,总计算次数大幅减少,大大简化了计算过程。
4 实证举例
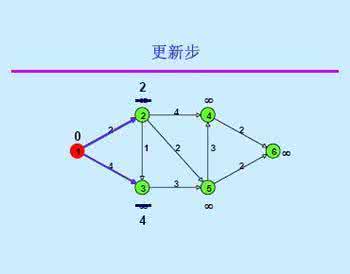
如图1所示,求图中顶点到的最短路径。
解一 用Dijkstra算法,计算过程如表1所示。
表示该顶点在这一步取得永久标号。由表1可知到的距离,到的最短路径为,计算步数为6,计算次数(表中标号个数)为21。
解二 用改进算法,计算过程如表2所示。
由表2同样可知到的距离,到的最短路径为,但表2中计算步数比表1减少,只需要5步,计算次数也减少为18。
5 结语
对Dijkstra算法的改进使得总计算步数由原来的步减少为不到步,计算次数得到大幅减少。同时实证检验进一步验证肯定了这一算法改进的优越性(步数由6步减少为5步,计算次数由21减少为18)。
参考文献
[1]温武,钟沃坚.离散数学及应用(第2版)[M].广州:华南理工大学出版社,2010.
[2]耿素云,曲婉玲,张立昂.离散数学[M].北京:清华大学出版社,2013.
[3]韦斯特.图论导引(第2版)[M].北京:电子工业出版社,2014.
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网