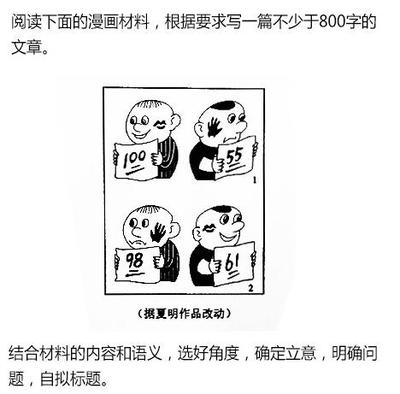
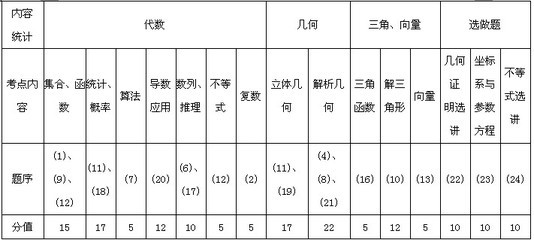
绝密★启用前
2013年普通高等学校招生全国统一考试(全国卷)
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页.考试时间120分钟.满分150分.
答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ卷答题卡和第Ⅱ卷答题纸规定的位置.
参考公式:
样本数据x1,x2,?xn的标准差
s?(x1?x)2?(x2?x)2???(xn?x)2
n其中x为样本平均数
球的面积公式 S?4?R2
第Ⅰ卷(选择题 共60分)
注意事项:
1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
2.第Ⅰ卷只有选择题一道大题.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.复数
A.1?2i(i是虚数单位)的虚部是 (B ) 1?i31 B. C.3 D.1 22
?2??1?,N?yy?x?1?1,则N?CRM?( D) x??
C.? D.?1,2? 2.已知R是实数集,M??x B.?0,2? ??A.(1,2)
3.现有10个数,其平均数是4,且这10个数的平方和是200,那么这个数组的标准差是(B)
A.1 B.2 C.3 D.4
4.设Sn为等比数列{an}的前n项和,8a2?a5?0则,S4?( A) S2
A.5 B.8 C.?8 D.15

- 1 -
5.已知函数f(x)?sin(2x?
的值是(D)
A.?6),若存在a?(0,?),使得f(x?a)?f(x?a)恒成立,则a???? B. C. D. 6342
( B ) 6.已知m、n表示直线,?,?,?表示平面,给出下列四个命题,其中真命题为
(1)????m,n??,n?m,则???
(2)???,????m,????n,则n?m
(3)m??,m??,则?∥?
(4)m??,n??,m?n,则???
A.(1)、(2) B.(3)、(4) C.(2)、(3) D.(2)、(4)
7.已知平面上不共线的四点O,A,B,C,若?3?2,等于(B)
A.1 B.2 C.3 D.4
8.已知三角形?ABC的三边长成公差为2的等差数列,且最大角的正弦值为
角形的周长是(D)
A.18 B.21 C.24 D.15
9.函数f(x)?lgx?
A.?0,1? B.?1,10? C.?10,100? D.(100,??)
10.过直线y?x上一点P引圆x?y?6x?7?0的切线,则切线长的最小值为(C) 223,则这个三21的零点所在的区间是(B) x
A.232 B. C. D.2 222
211.已知函数f(x)?x?ax?2b.若a,b都是区间?0,4?内的数,则使f(1)?0成立的概率是
(C)
- 2 -
A.3153 B. C. D. 8448
x2y2
12.已知双曲线的标准方程为??1,F为其右焦点,A1,A2是实轴的两端点,设P 为916
双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x?a分别交于两点M,N,若??0,则a的值为(B)
A.1692516 B. C. D. 5995
双曲线 x^2/9-y^2/16=1,
右焦点F(5.0),A1(-3,0),A2(3,0)
设P(x,y) M (a,m),N(a,n)
∵P,A1,M三点共线,
∴m/(a+3)=y/(x+3)
∴m=y(a+3)/(x+3)
∵P,A2,N三点共线,
∴n/(a-3)=y/(x-3)
∴n=y(a-3)/(x-3)
∵x^2/9-y^2/16=1
∴(x^2-9)/9=y^2/16
∴y^2/(x^2-9)=16/9
FM向量=(a-5,y(a+3)/(x+3))
FN向量=(a-5,y(a-3)/(x-3))
FM向量*FN向量
=(a-5)^2+y^2(a^2-9)/(x^2-9)
=(a-5)^2+16(a^2-9)/9
∵FM向量*FN向量=0
∴(a-5)^2+16(a^2-9)/9=0
25a^2-90a+81=0
∴a=9/5
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置.书写的答
- 3 -
案如需改动,要先划掉原来的答案,然后再写上新答案.
2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.
3. 第Ⅱ卷共包括填空题和解答题两道大题.
二、填空题:本大题共4小题,每小题4分,共16分.
13.如图所示的程序框图输出的结果为____2______.
14. 若一个底面是正三角形的三棱柱的正视图如下图所示,其
都在一个球面上,则该
球的表面积为_
_________.
点19? 3第14题图 如图。F,H是上下底的中心,O是FH中点。则:
AB=2 AE=√3, AF=2√3/3 OF=1/2
OA=√﹙AF2+OF2﹚=√﹙19/12﹚
球的表面积=4π﹙19/12
﹚=19π/3≈19.89675﹙面积单位﹚
向左转|向右转 第13题图
15.地震的震级R与地震释放的能量E的关系为R?2(lgE?11.4).2011年3月11日,日3
- 4 -
本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 10
16.给出下列命题:
①已知a,b都是正数,且,m32a?1a?,则a?b; b?1b
②已知f?(x)是f(x)的导函数,若?x?R,f?(x)?0,则f(1)?f(2)一定成立; ③命题“?x?R,使得x?2x?1?0”的否定是真命题;
④“x?1,且y?1”是“x?y?2”的充要条件.
其中正确命题的序号是 ①③ .(把你认为正确命题的序号都填上)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分) ?xxx已知向量a?(1,cos)与b?(3sin?cos,y)共线,且有函数y?f(x). 222
2?(Ⅰ)若f(x)?1,求?2x)的值; 3?2
(Ⅱ)在?ABC中,角A,B,C,的对边分别是a,b,c,且满足2acosC?c?2b,求函数
f(B)的取值范围.
解:(Ⅰ)∵a与b共线 ??
∴1?xx3sin?cos22cosyx
xxx1?1y?3sincos?cos2?sinx?(1?cosx)?sin(x?)?2222262
∴f(x)?sin(x?????3分 1?1?1,即sin(x?)? ????????????????4分 6262
2????1?2x)?cos2(?x)?2cos2(?x)?1?2sin2(x?)?1?? 33362)??
????????????????6分 (Ⅱ)已知2acosC?c?2b
由正弦定理得:
- 5 -
2sinAcosC?sinC?2sinB?2sin(A?C)
2sinAcosC?sinC?2sinAcosC?2cosAsinC∴cosA? 1?,∴在?ABC中 ∠A? ????????????????8分 32
?1f(B)?sin(B?)? 62
?2???5?∵∠A? ∴0?B?,?B?? ????????????????10分 33666
1?3∴?sin(B?)?1,1?f(B)? 262
3∴函数f(B)的取值范围为(1,] ????????????????12 2
18.(本小题满分12分)
已知等差数列?an?的前n项和为Sn,公差d?0,且S3?S5?50,a1,a4,a13成等比数列. (Ⅰ)求数列?an?的通项公式; (Ⅱ)设??bn??是首项为1,公比为3的等比数列,求数列?bn?的前n项和Tn. ?an?
解:(Ⅰ)依题意得
3?24?5?d?5a1?d?50?3a1? ????????????????2分 22??(a?3d)2?a(a?12d)11?1
解得??a1?3, ????????????????4分 d?2?
?an?a1?(n?1)d?3?2(n?1)?2n?1,即an?2n?1.???????????6分 (Ⅱ)bn?3n?1,bn?an?3n?1?(2n?1)?3n?1 ????????????????7分 an
Tn?3?5?3?7?32???(2n?1)?3n?1
3Tn?3?3?5?32?7?33???(2n?1)?3n?1?(2n?1)?3n????????9分 ?2Tn?3?2?3?2?32???2?3n?1?(2n?1)3n
- 6 -
3(1?3n?1)?3?2??(2n?1)3n
1?3
??2n?3n
∴
Tn?n?3n ????????????????12分
19.(本小题满分12分)
已知四棱锥A?BCDE,其中AB?BC?AC?BE?1,CD?面ABC,CD?2,BE∥CD,F为AD的中点.
(Ⅰ)求证:EF∥面ABC;
(Ⅱ)求证:面ADE?面ACD;
(III)求四棱锥A?BCDE的体积.
解:(Ⅰ)取AC中点G,连结FG、BG,
∵F,G分别是AD,AC的中点 C
D E D 1∴FG∥CD,且FG=DC=1 . 2
∵BE∥CD ∴FG与BE平行且相等
∴EF∥BG. ???????????2分 E
EF?面ABC,BG?面ABC
∴EF∥面ABC ???????????4分
(Ⅱ)∵△ABC为等边三角形 ∴BG⊥AC
又∵DC⊥面ABC,BG?面ABC ∴DC⊥BG
∴BG垂直于面ADC的两条相交直线AC,DC,
∴BG⊥面ADC . ????????????????6分
∵EF∥BG
∴EF⊥面ADC
∵EF?面ADE,∴面ADE⊥面ADC . ????????????????8分 (Ⅲ)连结EC,该四棱锥分为两个三棱锥E-ABC和E-ADC . C B
131333VA?BCDE?VE?ABC?VE?ACD???1??1????.?????????12分 34321264
- 7 -
另法:取BC的中点为O,连结AO,则AO?BC,又CD?平面ABC,
∴CD?AO,BC?CD?C , ∴AO?平面BCDE,∴AO为VA?BCDE的高,AO?(1?2)?13133. ,SBCDE??,?VA?BCDE????2223224
20.(本小题满分12分)
在某种产品表面进行腐蚀性检验,得到腐蚀深度y与腐蚀时间x之间对应的一组数据:
现确定的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求线性回归方程,再对被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好不相邻的概率;
(Ⅱ)若选取的是第2组和第5组数据,根据其它4组数据,求得y关于x的线性回归方
??程y4139,规定由线性回归方程得到的估计数据与所选出的检验数据的误x?1326差均不超过2微米,则认为得到的线性回归方程是可靠的,判断该线性回归方程是否可靠.
解:(Ⅰ)设6组数据的编号分别为1,2,3,4,5,6.设抽到不相邻的两组数据为事件A,从6组数据中选取2组数据共有15种情况:(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6),其中事件A包含的基本事件有10种. ????????????????3分
所以P(A)?1022?.所以选取的2组数据恰好不相邻的概率是. ?????????6分 3153
4139219219?10??,|?10|?2; ??????????????9分 13262626
4139379379?30??,|?16|?2; 13262626??(Ⅱ) 当x?10时,y?? 当x?30时,y
所以,该研究所得到的回归方程是可靠的. ????????????????12分
21.(本小题满分12分)
已知函数f(x)?ax?b在点(?1,f(?1))的切线方程为x?y?3?0. 2x?1
- 8 -
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)?lnx,求证:g(x)?f(x)在x?[1,??)上恒成立.
解:(Ⅰ)将x??1代入切线方程得y??2
∴f(?1)?b?a??2,化简得b?a??4. ????????????????2分 1?1
a(x2?1)?(ax?b)?2xf?(x)? 22(1?x)
f?(?1)?2a?2(b?a)2bb????1 . ????????????????4分 442
解得:a?2,b??2
2x?2 . ????????????????6分 2x?1
2x?2(Ⅱ)由已知得lnx?2在[1,??)上恒成立 x?1∴f(x)?
化简得(x?1)lnx?2x?2
即xlnx?lnx?2x?2?0在[1,??)上恒成立 . ????????????????8分 设h(x)?xlnx?lnx?2x?2, 222
h?(x)?2xlnx?x?1?2 x
x?1?2,即h?(x)?0. ????????????????10分 x∵x?1 ∴2xlnx?0,
∴h(x)在[1,??)上单调递增,h(x)?h(1)?0
∴g(x)?f(x)在x?[1,??)上恒成立 . ????????????????12分
22.(本小题满分14分)
实轴长为43的椭圆的中心在原点,其焦点F1,,F2在x轴上.抛物线的顶点在原点O,对称轴为y轴,两曲线在第一象限内相交于点A,且AF1?AF2,△AF1F2的面积为3. (Ⅰ)求椭圆和抛物线的标准方程;
(Ⅱ)过点A作直线l分别与抛物线和椭圆交于B,C,若?2,求直线l的斜率k.
x2y2
解(1)设椭圆方程为2?2?1(a?b?0),AF1?m,AF2?n ab
?m2?n2?4c2
??由题意知?m?n?43 ????????????????2分 ?mn?6??
解得c?9,∴b?12?9?3. 22
x2y2
∴椭圆的方程为??1 ????????????????4分 123
∵yA?c?3,∴yA?1,代入椭圆的方程得xA?22,
将点A坐标代入得抛物线方程为x2?8y. ????????????????6分
(2)设直线l的方程为y?1?k(x?22),B(x1,y1),C(x2,y2) 由?2 得x2?22?2(x1?22), 化简得2x1?x2?22 ????????????????8分 ??y?1?k(x?22)联立直线与抛物线的方程?, 2??x?8y
得x?8kx?162k?8?0 ∴x1?22?8k① ????????????????10分 2
??y?1?k(x?22)联立直线与椭圆的方程? 22??x?4y?12
得(1?4k)x?(8k?162k)x?32k?162k?8?0 2222
162k2?8k∴x2?22?② ????????????????12分 1?4k2
162k2?8k?22?22 ∴2x1?x2?2(8k?22)?21?4k
整理得:(16k?42)(1?2k)?0 1?4k2
- 10 -
∴k?22 ,所以直线l的斜率为 . ????????????????14分 44
- 11 -
 爱华网
爱华网