tubianlun
突变论
catastrophe theory
研究不连续现象的一个新兴数学分支,也是一般形态学的一种理论,能为自然界中形态的发生和演化提供数学模型。突变论在数学上属于微分流形拓扑学的一个分支,是关于奇点的理论。因为英文 catastrophe一词的原意为突然来临的灾祸,所以也有把它译作灾变论。突变论一般并不给出产生突变机制的假设,而是提供一个合理的数学模型来描述现实世界中产生的突变现象,对它进行分类,使之系统化。突变论特别适用于研究内部作用尚属未知、但已观察到有不连续现象的系统。
简史 突变论是20世纪60年代末法国数学家为了解释胚胎学中的成胚过程而提出来的。1967年托姆发表《形态发生动力学》一文,阐述突变论的基本思想,1969年发表《生物学中的拓扑模型》,为突变论奠定了基础。1972年发表专著《结构稳定与形态发生》,系统地阐述了突变论。70年代以来,E.C.塞曼等人提出著名的突变机构,进一步发展了突变论,并把它应用到物理学、生物学、生态学、医学、经济学和社会学等各个方面,产生了很大影响。
研究方法 从I.牛顿和G.W.莱布尼兹时代以来得到很大发展的微积分学,一般只考虑光滑的连续变化的过程,而突变论则研究跳跃式转变、不连续过程和突发的质变。突变论的基础是结构稳定性。结构稳定性反映同种物体在形态上千差万别中的相似性。例如,人的面貌虽因岁月流逝而发生变化,但仍存在区别于他人的特征。结构稳定的丧失,就是突变的开始。突变论的基本概念是静态模型,它把形态按结构稳定特征分类。至于描述结构变化的动力学理论,至今仍不完备。
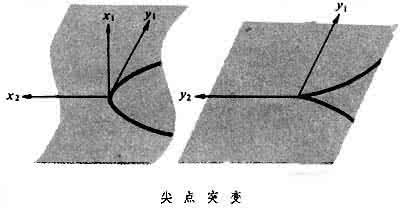
突变论的数学基础是奇点理论和分岔理论。最原始的奇点是微积分中实变函数的极大极小点(临界点)。这种函数可看成是实数空间 (坐标)到实数空间(坐标)的映射。而平面(1,)到平面(1,)的光滑映射可用一对函数 1=1(1,2),2=2(1,2)表示。1955年H.惠特尼在研究这种映射的特点时,得出两类一般奇点一类是折叠,可用公式=,=表示。把球面投射到平面上,赤道上的点产生的奇点就是这种奇点另一类是尖点,局部坐标可写成=+1,=。把空间曲面1=+投影到平面(,)上,平面上有一半立方抛物线,在原点处有一个尖点 (见图[尖点突变])。曲线把平面分成两部分,较小部分的原像均由三点构成,而较大部分只由一个点构成。在尖点处映射引起突变,这是突变论所研究的最常见的一种突变。惠特尼证明,尖点是稳定的,也就是在这种映射附近的映射在适当的地方也有同类的奇点。
托姆把惠特尼的奇点理论加以推广,应用到突变论中他研究→的奇点分类问题。这里是描述系统状态的参数(称为状态参数或内部参数)的数目,而是控制参数(又称外部参数)的数目。随着控制参数的改变,状态参数可能产生突变,在突变处控制参数值称为突变点。通常可以任意大,但R(可取作四维时空欧氏空间,反映时空中进行的控制过程。
静态模型 静态模型是一族势函数:→,其中是状态空间的子集,包含原点的邻域,参数 属于控制空间中原点的邻域。 状态空间可用与过程有关的状态参数来表示,控制空间则可用控制过程中控制参数来描述。当维数≤4时,具有标准势函数的静态模型就是初等突变。它可作为各种自然过程的定性模型。静态模型已被推广成代谢模型。表[余维数≤4的初等突]≤4的初等突" class=image>[变]中列出了所有初等突变。
除了基本的初等突变外,托姆还给出高阶突变,为建立一般突变论奠定了初步的基础。他描述的鸡胚发育模型和蟹状星云、超新星爆炸残余模型都属于一般突变论的范畴,但还没有建立起一般的数学理论。
应用 突变论应用范围极为广泛。在数学、力学和物理学中,借助突变论不仅能加深对已有定律的认识,而且还能得到一些新的成果。例如,利用突变论找到了光的焦散面的全部可能的形式。在生物学和社会学中,许多现象很难用其他数学方法处理,但用突变论可得到理想的数学模型。如捕食者与被捕食者系统中群体消长情况,用微分方程不能得出满意的解释,而用突变论预测的结果却与实验符合。利用突变论有可能预测系统的许多定性性态,甚至在不知道系统的描述采用什么样的微分方程,或者不知道怎样求解这些微分方程的情况下,也能获得结果。而且这种预测是在少数几个假设的基础上完成的。例如对于胚胎形成过程、心脏搏动、大脑机制、船舶稳定性等都曾用突变论建立过相当的数学模型,并取得一定的成效。
参考书目
P.T.桑德斯著,凌复华译:《灾变理论入门》,上海科学技术文献出版社,上海,1983。(P.T.Saunders, An Introduction to Catastrophe Theory,Cambridge Univ.Press,1980.)
R.Thom,Stabilit Structurelle et Morphonse,Read-ing,Mass.,Benjamin,1972.
胡作玄
以上就是网友分享的关于"突变论"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网