韦达定理的应用 巧用韦达定理的推论

韦达定理揭示了一元二次方程的两根之和、之积与系数的关系，然而在学习中，我们经常还会遇到两根之差、之比、平方和等问题，如果能将它们与系数建立起来关系，直接用这种关系来解题，岂不妙哉？下面是韦达定理的三个推论，它会给大家带来惊喜．

推论一 设x1、x2是一元二次方程ax2＋bx＋c＝0(a≠0)的两个实根，则。

推论二 设x1、x2是一元二次方程ax2＋bx＋c＝0(ac≠0)的两个实根，令,则。

推论三 设x1、x2是一元二次方程ax2＋bx＋c＝0(a≠0)的两个实根，则。

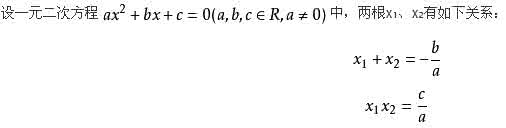
利用上述推论来解题，显得简捷、明快、直观，对提高同学们的解题能力很有帮助，下面举例说明它们的应用．

　　一、求值

例1 已知x1、x2为方程2x2＋2x－1＝0的二根，则|x1－x2|的值为____

解: 由推论一，得：|x1－x2|=

例2 设x1、x2是方程x2＋6x＋q＝0的两根，且3x1＋2x2＝0，则q＝____．

解:由3x1＋2x2＝0，得。　由推论二，得：　∴q＝－216．

例3 已知关于x的方程x2－(k＋1)x＋k＋2＝0的两实根的平方和等于6，求k的值．

解 设方程x2－(k＋1)x＋k＋2＝0的两根为x1、x2，

∴，由题意知k2－3＝6，∴k2＝9，k＝±3．

由于当k＝3时，原方程无实根，∴k＝3应舍去．故k的值为－3．

　　二、求系数间的关系

例4 如果方程x2＋px＋q＝0的一根为另一根的2倍，那么p，q所满足的关系式是____．

解：因为，由推论二得，即。

例5 方程x2＋px＋q＝0的两根之差与x2＋qx＋p＝0的两根之差相等，则p，q的关系式是____．      (A)p＝q； (B)p＋q＝－4； (C)p＝q或p＋q＝－4； (D)无关．

解 设方程x2+px+q=0的两根为α，β，方程x2+qx+p=0的两根为α′，β′，则，。由题意得=，　

即(p－q)(p＋q＋4)＝0．∴p＝q或p＋q＝－4．故选(C)．

三、求最值

例7 已知x1、x2是方程x2－(k－2)x＋(k2＋3k＋5)=0的两个实数根(其中k为实数)，则的最大值是          。

解：∵

　　又∵△＝(k－2)2－4(k2＋3k＋5)≥0，

　　即3k2＋16k＋16≤0，∴解得

　　∴当k=-4时，的最大值是18。

爱华网本文地址 » http://www.aihuau.com/a/342851/937035520207.html