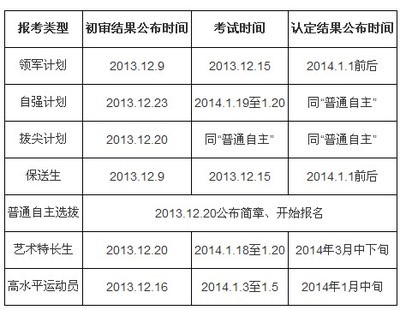
2014年西南财经大学自主招生考试(由摩西摩西整理)
说明:数学每题12分,作文40分
1.已知函数f(x)=13x+mx2-3m2x+1,m3属于R,
(1)若m=1,求曲线y=f(x)在点(2,f(2))处的切线方程
(2)若函数f(x)在区间(-2,3)上是减函数,求m的取值范围
区间(-2,3)上是减函数,则??m??2,解得??3m?3m≤-2.
综上所述,实数m的取值范围是m≥3或m≤-2.…(13分)
12.在△ABC中,a,b,c是∠A,∠B,∠C的对边,a=4,b=6,cosA=- 3
1
(1)求c
(2)求cos(2B-)的值
解得:c=2或c=-6(舍去),
则c=2;
(2
?4
3∵B为锐角,∴
cosB=?sin2B?
)
3.某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会 2
超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数p=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
解:(1)当0<x≤100时,p=60;
当100<x≤600时,
p=60-(x-100)×0.02=62-0.02x
60,0?x?100??p?? ?62?0.02x,100?x?600
(2)设利润为y元,则
当0<x≤100时,y=60x-40x=20x;
当100<x≤600时,y=(62-0.02x)x-40x=22x-0.02x2
20x,0?x?100??y???22?0.02x,100?x?6002
当0<x≤100时,y=20x是单调增函数,当x=100时,y最大,此时y=20×100=2 000;
2+6 050,当100<x≤600时,y=22x-0.02x2=-0.02(x-550)
∴当x=550时,y最大,此时y=6 050.
显然6050>2000.
所以当一次订购550件时,利润最大,最大利润为6050 3
元.

4.已知m∈R,函数f(x)=(x2+mx+m)·ex.若函数f(x)存在极大值,并记为g(m),求g(m)的表达式
(2)f′(x)=(2x+m)ex+(x2+mx+m)ex=(x+2)(x+m)ex, 令f′(x)=0,得x=-2或-m, 当m>2时,则-m<-2,
当x=-m时,f(x)取得极大值me-m,
当m=2时,f′(x)=(x+2)2ex≥0,f(x)在R上为增函数,∴f(x)无极大值. 当m<2时,则-m>-2.
当x=-2时,f(x)取得极大值(4-m)e-2,
4
?me,m?2?g(m)???(4?m)e,m?2?m?2
5.把在标有1-8号数字的标牌中抽取一张后放回的事件称为一次随机实验,pn是n次实验中抽取的8号标牌的次数为奇数的概率,求:pn
6.材料:记者关于雾霾问题的调查资料
要求:以“经济发展与环境保护”为话题,从你感受最深的角度,自拟题目,写一篇不少于600字的议论文
5
爱华网 www.aIhUaU.com欢迎您转载
 爱华网
爱华网