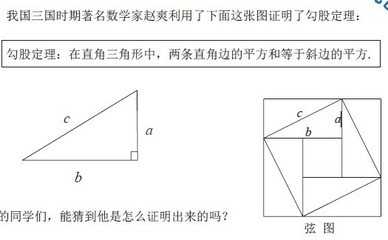
借勾股逆定理找直角三角形解题湖北省黄石市下陆中学 周国强#TRS_AUTOADD_1310450867379 {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1310450867379 P {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1310450867379 TD {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1310450867379 DIV {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1310450867379 LI {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}/**---JSON--{"":{"margin-top":"0","margin-bottom":"0"},"p":{"margin-top":"0","margin-bottom":"0"},"td":{"margin-top":"0","margin-bottom":"0"},"div":{"margin-top":"0","margin-bottom":"0"},"li":{"margin-top":"0","margin-bottom":"0"}}--**/DIV.MyFav_1310450869082 P.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310450869082 LI.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310450869082 DIV.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310450869082 DIV.Section1{page: Section1}DIV.MyFav_1310450869082 OL{MARGIN-BOTTOM: 0cm}DIV.MyFav_1310450869082 UL{MARGIN-BOTTOM: 0cm}某些问题如果借助勾股定理的逆定理(简称勾股逆定理)来解方便简捷
一、求周长
例1 如图⑴,△ABC中,AB = 5,AC = 13,BC边上的中线AD=6,求△ABC的周长.
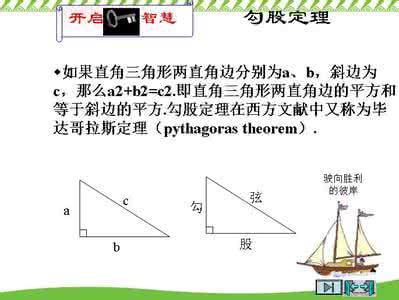
解析:显然必须先求出BC的长,但因△ABC 不是直角三角形而无法求出BC的长,为把中线AD与△ABC的边AB、AC进行有效的沟通,需将已知线段AB、AC、AD转移到同一三角形的边上,运用勾股逆定理寻找直角三角形来解决.延长中线AD一倍至E,连CE,知△CDE≌△BDA(SAS),从而CE=AB=5.这样,就把已知线段AB、AC、AD全部集中在△ACE中了,因为CE+AE=5+12=13=AC,所以△ACE是直角三角形且∠E为直角,然后在Rt△CDE中易求得CD的长为,从而求得△ABC的周长为18+2.
二、求面积
例2 如图⑵ 是一块三角形空地,现从中征用一块三角形土地(△ACD)用于建房,经测量AB=250m,BC=240m,AC=70m,CD=50m,且∠ADC=90.请你计算一下剩余空地的面积是多少(精确到1m).
解析:因为AC+BC=70+240=62500=250=AB,所以△ABC是直角三角形,且∠ACB=90,因为△ABC的面积为AC×BC=70×240=8400(m);△ACD的面积为CD×AD =×50×=25=500,所以剩余空地的面积为8400-500≈7150(m).
三、求角度
例3 如图3,△ABC中,∠ACB=90,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求∠BPC的度数.
解析:注意到PA=6,PB=2,PC=4,因它们不是同一三角形的三边长,也不是一组勾股数,所以须以这些线段长为依据寻找新的直角三角形,运用勾股逆定理求出问题的答案.由于△ACB是等腰直角三角形,将△CPB绕点C顺时针旋转90至△CQA,则△CQA≌△CPB(SSS),且△PCQ也是等腰直角三形.连PQ,因CQ=CP=4,∠QCP=90,知PQ= 4;这样,在△APQ中,因为AQ+PQ=2+(4)= 36 = PA,所以△APQ是直角三角形且∠AQP=90,所以∠BPC=∠AQC=∠AQP+CQP=90+45=135.
四、判形状
例4 如图4,已知,∠ABE=30,∠A=∠EBC=60,设AB长为m,BC长为n,CD长为p,且m、n、p满足关系式|m-4| +(n-2)+= 0,若DE=3,试问:四边形BCDE是何种特殊四边形?为什么?
解析:因为|m-4| +(n-2)+= 0 ,所以m=4,n=2,P=,即AB=4,BC=2,CD=,由∠ABE=30,∠A=∠EBC =60,知BE⊥AD,所以AE=AB=2,从而BE= BC =2,所以△BCE是等边三角形(有一个角是60的等腰三角形是等边三角形),所以CE=2,在△CDE中,因为CD+DE=()+3=12 =(2)= EC,所以∠CDE=90,从而CD∥BE,又DE不平行于BC,故四边形BCDE是直角梯形.
爱华网本文地址 » http://www.aihuau.com/a/356851/332900945642.html

 爱华网
爱华网