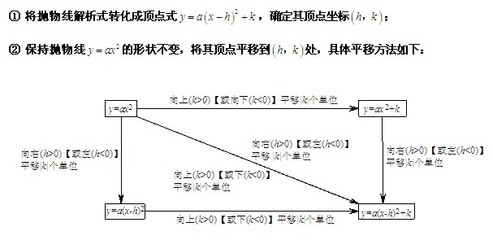
二次函数综合练习<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />
一. 填空题:
1.直角坐标平面内所有的点与___________________是一一对应的。
2.已知P(a,b),若a<0,b>0则P在第______象限内;若a=0,b<0,则P在______;若a=--b,则P在__________.
3.已知P(5,-3),点P关于x轴的对称点P1的坐标是_________,点P关于y轴的对称点P2的坐标是_________,点P关于原点的对称点的坐标是___________.
4.直线y= -2x+3与x轴交点的坐标是_______,与y轴交点的坐标是________
5.直线<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" />与直线的交点的坐标为_________。
6.抛物线y=x2—x+m,当m______时与x轴没有公共点;当m_______时与x轴只有一个公共点;当m_______时与x轴有两个公共点。
7.若一元二次方程ax2+bx+c=0有两个不相等的实数根,则二次函数y=ax2+bx+c的图象与x轴的交点的坐标是_________________
8.若二次函数y=x2—8x+m的顶点在x轴上,则m=______,y的取值范围是___________.
9.在x轴上与原点的距离均为a的两点坐标是__________和________。
10.函数的自变量x的取值范围是__________
11.函数的自变量x的取值范围是____________
12.池内有水<?xml:namespace prefix = st1 ns = "urn:schemas-microsoft-com:office:smarttags" />100m3,每小时流出4m3,则池内剩下水V(m3)与流水时间t(小时)的函数解析式是____________________________。
13.函数的自变量的取值范围是_____________
14.y-2与x成正比例,且当x= -1时,y=7则y与x间的函数关系式是____________
15.已知xy=5,则y与x之间是_______函数关系,函数的图象叫做_____________。
16.平行四边形的面积一定时,它的一边和这边上的高是____________函数关系。
<?xml:namespace prefix = w ns = "urn:schemas-microsoft-com:office:word" />17.菱形的边长为5,一个内角为60º,它的对角线与坐标轴重合,则各顶点坐标是_____________________________________________.
18.已知一次函数过A(3,1)且在y轴上的截距是5,则它的函数关系式__________.
19.函数y=-3x+4的图象是通过_________象限的直线。
20.函数y=kx+(2k+4)的图象过原点,则k=_______
21.函数的对称轴是_________,顶点坐标是____________。
22.抛物线y=3 - 2x - x2的顶点坐标是_________,它与y轴的交点坐标是__________,它与x轴的交点坐标是____________。
23,函数y=x2 - 2x+3的最小值是__________,此时x__________。
24,如图,二次函数y1与一次函数y2的图象交于B(3,0),C(0,3)点,二次函数图象与坐标轴交于A(--1,0)、B、C三点,且对称轴平行于y轴,则当x________时,y1y2都随增大而减小;当x_______时,y1·y2<0

二. 选择题1已知点P1(-4,3)和P2(4,-3),则P1和P2 ( )A.关于轴对称B关于轴对称C关于原点对称D以上都不对
2.已知点P的坐标为(2tg45º,sin30º),则P点关于x轴对称的点的坐标是:A(-2,1/2)B(2,-1/2)C(2/3,-1/2)D(2,-3/2)
3.已知点A(1,2),AC垂直于x轴,交x轴于C点,则C点的坐标是:()A.(0,0)B(1,0)C(2,0)D(2,1)
4.函数中自变量x的取值范围是:()A.x≠4的一切实数。B x>4或x<--4 C.- 4< x < 4 D x≠±4的一切实数。
5.下面哪个函数是正比例函数是:()y=2x By=1/2x C y=x2 D y=2x-1
6.设y+b与x+a成正比例,则y是x的:()A.正比例函数或一次函数B一次函数C.反比例函数D二次函数
7.若一次函数的图象y=kx+b经过第二、三、四象限,则k和b的取值范围是:()A.k>0且b>0 B k<0且b>0 Ck<0且b<0 D k>0且b<0。
8.不论x为任何实数,函数y=ax2+bx+c的图象和x轴没有交点的条件是:()A.△>0B △<0 C△=0 D △≤0
9.已知点(2,5),(4,5)是抛物线y=ax2+bx+c上的两点,那么,这个抛物线的对称轴方程是:()A.x=-b/a B.x=1 C.x=0 D.x=3.
三. 计算题。
1已知y=y1 - y2, y1与x的算术平方根成正比例,y2与x的平方成反比例,且当x=1时,y=0;当x=2,时y=31/4,求y=y1-y2的解析式。
2.在直角坐标系内,直线y=kx+b经过三点,A(2,0),B(0,2),C(m,3)。
(1) 求这条直线的函数关系式,并画出这条直线。求m的值和AC的长度。(3)求∠OCA的正弦值。
3.已知一次函数y=(3m+2)x — (4—n),求分别满足的m,n值:(1)图象过第一、二、四象限。(2) y随x值的增大而增大。
(3)图象与y轴的交点在x轴的下方. (4)图象与x,y轴的交点坐标分别为(-2,0),(0,5)
4.求直线y=x-3与双曲线y=-2/x的交点,并画出它们的图象。
5.一个正比例函数和一个一次函数,它们的图象都经过点P(-2,1),且一次函数的图象在y轴上截距为3。(1)求这两个函数的解析式. (2)在同一个坐标系内分别画出这两个函数的图象。(3)求这两个函数的图象与y轴围成的三角形的面积。
6.已知点A(a,1)和点B(7,b)是直线y=-x+2上的两点。(1)求a和b值。(2)若直线AB交x轴于C,求SΔAOD和SΔAOB。
7.二次函数的图象过(3,2)和(0,-1)两点,对称方程是x=1,求这个二次函数的解析式。
8.把函数y=x2/2的图象向下平移3个单位,得到函数yˊ,再把函数向右平移2个单位,得到函数y〞.试写出函数y〞的解析式。
9.已知二次函数y=--x2+2x+3,当x取什么值时,二次函数y有最大值或最小值?当x取什么值时,y的值随着x值的增大而增大?
10.求函数的解析式:(1)二次函数有最小值—1,当x=0时,y=1,它的图象的对称轴x=1。(2)二次函数当x=2时,y=-12,它的图象与y轴交点的纵坐标和x轴的一个交点的横坐标都为—8。(3)二次函数y=ax2+bx+c的图象与x轴的两交点间的距离为4,并过(2,-3)。
11.抛物线y1=ax2+bx+c 与y2=x2 的图象的形状完全一样,只是位置不同,抛物线y1过(0,-6),(3,6),求它的顶点坐标。
 爱华网
爱华网