关键词:蚁群算法 运输问题 大规模
中图分类号:TP301.6 文献标识码:A 文章编号:1007-9416(2016)11-0135-01
运输问题是一类应用广泛的现实问题。康特洛维奇和希契科克对于该问题进入了深入的研究,故而运输问题又称为“康-希问题”。对于运输问题,最经典的数学模型如下:设某种物资有m个产地Ai,其产量分别为ai,i=1,2,...,m。有n个销地Bj,其销量分别为bj,j=1,2,...,n。已知由产地Ai到销地Bj运输单位物资的运价为cij。现在要确定总运费最小的运输方案。本文主要考虑现实中粮食收购点向粮食存储仓运输的问题。
1 推广运输问题及其数学模型
用决策变量xij表示产地Ai到销地Bj的运量,对应的数学模型可以归结为如下:
由上可见,运输问题可以归结为一个线性规划问题。当然可以用经典的单纯形法求解,但由于其本身的特性,一般利用表上作业法,从而更简单更有效的解决。
本文针对现实中粮食收购点向粮食存储仓运输的问题,由于问题本身的特殊性,即没有产销的约束,所有的粮食都可以被收购。同时,不同的粮食存储仓收购的价格不一样,与粮食收购点的路程不一样会导致运输成本不一样。设S={s1,...,sm}是所有粮食收购点的集合,D={d1,...,dn}是所有粮食存储仓的集合。S,DV,其中V是所有的节点结合。G=(S∪D,Ω)是一个路径的网络,ΩE是所有链接S,D两个集合的所有可行路径,Volij是Si到Dj的运输量,VCij是对应的可变成本。对应的数学模型为:
其中Volij表示从节点i到节点j的运输量。Bij是一个0,1变量,用来表示从节点i到节点j的边是否被选取。E表示网络中的所有节点,T表示既不是起点也不是终点的节点集合。约束条件主要是对于每一个节点而言,必须是进出平衡的。而最短路进问题随着路径的增多,起计量指数增加。为了求解这个优化问题,引入智能算法-蚁群算法来解决。
2 蚁群算法
蚁群算法是一种基于蚂蚁在寻觅食物的过程中对于路径选择优化而提出的一种群智能算法,最初主要对于解决TSP问题。基本蚁群算法寻优机制包含两个基本阶段:适应阶段和协作阶段。在适应阶段,各候选解根据积累的信息不断调整自身结构,路径上经过的蚂蚁越多,信息量越大,则该路径越容易被选择;时间越长,信息量越小;在协作阶段,候选解之间通过信息交流,以期望产生性能更好的解。
bi(t)表示t时刻位于元素i的蚂蚁数目;τij(t)为t时刻路径(i,j)上的信息量;N表示TSP的规模;dij表示相邻两个城市之间的距离;m为蚁群中蚂蚁的总数目,则m=Σ(bi(t)|i=1,2,…,n);pkij(t)表示在t时刻蚂蚁k由元素(城市)i转移到元素(城市)j的状态转移概率;
在初始时刻各条路径上信息量,并设τij(0)=const,蚂蚁k(k=1, 2,…,m)在运动过程中,根据各条路径上的信息量决定其转移方向。这里用tabuk(k=1,2,…,m)来记录蚂蚁k当前所走过的城市,集合随着tabuk进化过程作动态调整。在搜索过程中,蚂蚁根据各条路径上的信息量及路径的启发信息来计算状态转移概率。
Allowedk={C-tabuk}表示蚂蚁k下一步允许选择的城市;α为信息启发式因子;β为期望启发式因子,其值越大,则该状态转移概率越接近于贪心规则;启发函数ηij(t)=1/dij;显然,该启发函数表示蚂蚁从元素(城市)i转移到元素(城市)j的期望程度。
为了避免残留信息素过多引起残留信息淹没启发信息,在每只蚂蚁走完一步或者完成对所有n个城市的遍历后,要对残留信息进行更新。由此,t+n时刻在路径(i,j)上的信息量可按如下规则进行调整:
式中,ρ表示信息素挥发系数,则1-ρ表示信息素残留因子,为了防止信息的无限积累,ρ的取值范围为:[0,1);△τij(t)表示本次循环中路径(i,j)上的信息素增量,初始时刻△τij(0)=0,△τijk(t)表示第k只蚂蚁在本次循环留在路径(i,j)上的信息量。
3 改进蚁群算法求解推广运输问题
3.1 蚁群算法的改进
传统的蚁群算法都是蚂蚁随机的从出发地搜索到目的地。本文基于两边向中间搜索的策略,在产地到销地各放置相应个数的蚂蚁,同时向中间搜索。搜索过的节点放入禁忌表,如果有两个蚂蚁搜索到同一个节点,本次搜索过程完毕。这样通过两组蚂蚁独立的搜索,一方面增强了搜索的随机性,一方面加快了算法收敛的速度,可以更快更优的求解。
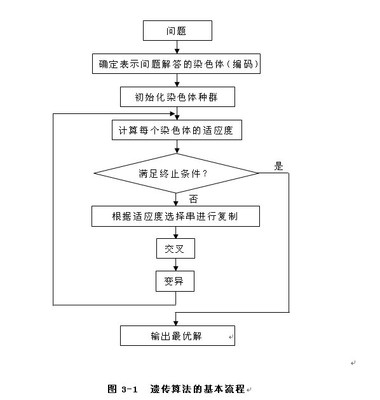
3.2 算法流程
Step1:利用改进蚁群算法,不考虑运输量,求解最短路径。
Step2:按产地到销地最大化配送。已空的产地或则已满的销地划去。
Step3:重复1,2,直到所有的产销配送完成。
通过问题求解,我们会发现,其实传统的运输问题是推广问题的一种特殊情况,即考虑产销地的单位物资运价是固定的。推广之后,更有灵活性和实际意义,因为一般只可以知道单位物资单位路程的运价。
参考文献
[1]马宇红,姚婷婷,张芳芳.多车场多车型车辆调度问题及其遗传算法[J].数学的实践与认识.2014,(2):107-114.
[2]谢金宝.有供需要求运输问题的数学模型及算法[J].中国铁道科学,2009,(5).
[3]张开碧,张洋川,万素波,白银.一种改进的竞争型蚁群算法在TSP问题中的应用磁[J].计算机与数字工程,2016,(3).
[4]何小虎.基于改进蚁群算法在粮食物流配送路径优化的应用研究[J].电子设计工程,2016,(9):39-41.
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网