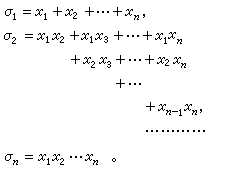整式不等式

multinomial inequality
有理不等式中的一类。两个整式由不等号连结而成的不
等式。这两个整式次数的较大者定义为不等式的次数。如2x+3>0为一次不等式,x2+3x>2,x2+y2≥2xy为二次不等式。
在解不等式问题中,最基本的整式不等式有:
①一元一次不等式。两边都是一元一次整式的不等式,通过同解变形,化为标准形式ax+b>0,x表未知数,若a≠0,则a>0时,解得-<x<+∞;a<0时,解得-∞<x<-。若a=0,则b>0时,解是所有实数;b<0时无解。
②一元二次不等式。两边都是一元二次整式的不等式,同解变形化为标准形式ax2+bx+c>0。若a>0,取判别式Δ=b2-4ac,则当Δ>0 时,解得 x< 或 x> ;当Δ=0时,x为除-2外所有实数,当△<0时,解得;当△≤0时,无解。若a=0,不等式bx+c>0同解,按一元一次不等式处理。
③二元一次不等式。有代表性的一种形式是ax+by+c>0,a,b,不全为零,x,y,为未知数,每个解是一个序偶(x,y),对应坐标平面上一个点,解集对应直线ax+by+c=0一侧的半个平面,b>0时上侧,b<0时为下侧。以上就是网友分享的关于"整式不等式"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
爱华网本文地址 » http://www.aihuau.com/a/372751/497214253093.html
更多阅读
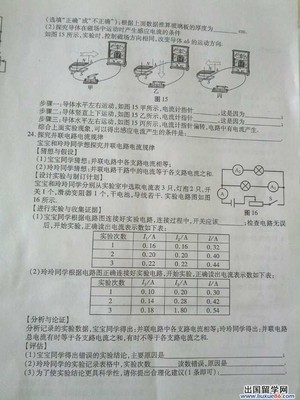
中考试题专题整式一、选择题1.(2009年台湾)已知(19x-31)(13x-17)-(13x-17)(11x-23)可因式分解成(ax+b)(8x+c),其中a、b、c均为整数,则a+b+c=?A.-12B.-32C.38D.72。【关键词】分解因式【答案】A2.(2009年台湾)将一多项式[(17x2-3x+4)-(a
第一章 整式的运算1、 整式:只含“×”“÷”运算的代数式叫单项式含“×”“÷”“+”“—”的代数式叫多项式2、 整式的加减:(1)去括号时,括号前是“+”时,直接去括号。(2)去括号时,括号前是“—”时,括号内符号要变号。(3)整式加减的实质是合
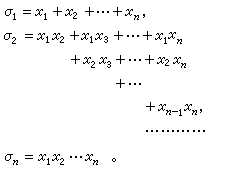
代数式:有理式(整式和分式)和无理式(根式),多项式和单项式代数式代数式:由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式。例如:ax+2b,-2/3,b^2/26,√a+√2等。注意:1、不包括

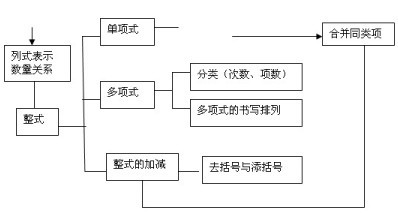
《2.1整式》(第一课时)教学设计2.1整式-------用字母表示数一、教材分析本节课内容属于“数与代数”领域,是在学习了用字母表示数、简单的列式表示实际问题中的数量关系和简易方程的基础上,进一步研究用含有字母的式子(整式)表示实际问

《整式的加减》(第三课时)教学设计中山市石岐启发中学孔进教学目标1.复习巩固合并同类项和去括号法则2.进一步经历用字母表示数量关系的过程,培养符号意识3.会进行整式加减的运算,并能说明其中的算理4.经历探索整式加减运算法

 爱华网
爱华网