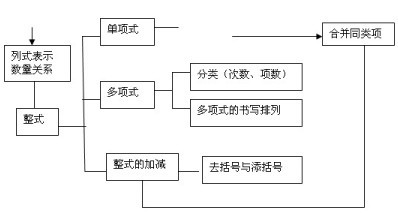
三、知识要点
1.整式的概念
代数式★★ 用运算符号和括号把数或表示数的字母连接而成的式子叫做代数式(algebraic expression).单独一个数或字母也是代数式.
★要点提示★
1.代数式及写法
⑴代数式中用到乘号,若是数字与数字相乘,“×”号不能省略;若是数字与字母相乘或字母与字母相乘,通常乘号写作“·”或省略不写,如a×b写成a·b或ab.
⑵数字与字母相乘,将数字写在字母的前面(1省略不写).如3a一般不写成a3;1a写成a.
⑶分数与字母相乘,若分数是带分数,要化成假分数.如
⑷几个字母相乘,一般按26个字母顺序书写.如ba一般写成ab.
⑸除法运算相乘方式形式.如x÷2写成x/2.
⑹若所列代数式表示一个有单位的结果时,若代数式是积或商的形式,则单位直接写在代数式后面;若代数式是和或差的形式,要先把代数式用括号括起来,再将单位名称写在式子后面.如(a+3b)米.
⑺代数式中只含运算符号(+,-,×,÷,乘方,开方),不含关系符号(如=,>,<,≈,≠等).
⑻数的运算律同样适用代数式.
2.代数式的分类
3.列代数式
⑴在同一个问题中,不同的数量关系必须用不同的字母表示.
⑵按“先读先写”的原则列代数式.
⑶抓住关键词语,如:“大”、“小”、“多”、“少”、“和”、“差”、“积”、“商”、“倍”、“分”等.
⑷分清运算顺序,注意读出关键词语的断句及括号的恰当使用.
代数式的值★★ 用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.
★要点提示★
1.一般地,代数式的值不是固定不变的,它是随着代数式中字母取值的变化而变化.
2.代数式中字母的取值必须保证代数式有意义,或代数式所表示的实际问题有意义.如a表述学生数,则a只能取正整数.
3.求代数式的值一般分“化简”、“代入”、“计算”等步骤.化简:一是代数式的化简,二是字母值的化简.代入是用数值代替代数式中字母,代入时原来省略的乘号要添上;代入有直接代入,有时也整体代入;代入是重要一步,要规范书写,如:“当x=…时,2x+3=…”.计算时要分清运算的种类,还要注意运算的顺序.
单项式★★ 由数与字母的积或字母与字母的积所组成的代数式叫做单项式(monomial).单项式中的数字因数叫做这个单项式的系数(coefficient).单项式中所有字母的指数的和叫做这个单项式的次数(degree).
★要点提示★
1.由数与字母的积所组成的代数式叫做单项式.这里的“数”可以是现在所学的任何数.
3.如果一个单项式只含有字母因数,它的系数就是1或-1,例如axy的系数是1,-n的系数是-1.
4.当字母的指数为1时,省略不写,但在确定单项式的次数时,不能忽略,比如-3x2y,它的次数是3而不是2.我们把常数项的次数看作0.
5.单项式有五中情形:①单独一个数,如3,-5等;②单独一个字母,如m,x等;③数与数的积,如2π等;④字母与字母的积,如xy2等;⑤数与字母的积,如2xy等.
多项式★★ 由几个单项式的和组成的代数式叫做多项式(polynomial),在多项式中的每个单项式叫做多项式的项(term),不含字母的项叫做常数项(constant term),次数最高项的次数就是这个多项式的次数.
多项式的排列
降幂排列 把一个多项式按某一个字母的指数从大到小的顺序排列,叫做这个多项式按这个字母的降幂排列.
升幂排列 把一个多项式按某一个字母的指数从小到大的顺序排列,叫做这个多项式按这个字母的升幂排列.
★要点提示★
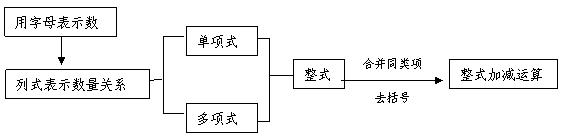
1.多项式的每一项都包括它前面的符号.
2.多项式 3x4+5x3-x2+2叫做四次四项式,各项的名称分别
为:3x4叫做四次项,5x3叫做三次项,-x2叫做二次项,2叫
做常数项.
3.在对多项式进行“升幂”或“降幂”排列时,要连同各项前面的符号一起移动,某项前面是“+”,在第一项时,正号“+”可以省略,其它位置不能省略.
4.含有两个或两个以上字母的多项式,注意“按某一字母”排列.
整式 单项式,多项式统称为整式(integral expression).
 爱华网
爱华网