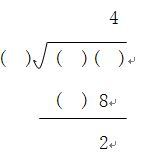想要迅速提高GMAT数学的考试成绩,考生需要在熟练掌握GMAT数学备考要点的基础上,掌握一些实用的解题技巧,以提高GMAT数学的备考效率。下面就来为大家简单介绍一下GMAT数学考试中余数题型的解题方法,希望能够为考生备考GMAT数学带来帮助。
很多同学对余数题都不知如何下手,其实前辈们已经为我们总结了很多方法,为方便大家,我在这里给大家汇总2种最常用,同时也比较便捷的解题思路,希望能帮大家顺利通过考试。注:版权归原作者所有,俺只是负责宣传,:)
如果看不懂推理过程,也不必计较,直接记住方法就可以了。同时希望大家顺手up下,以便帮助后面的同学。
第一种、设通项式求解。
通项S,形式设为S=Am+B,一个乘法因式加一个常量
系数A必为两小通项因式系数的最小公倍数
常量B应该是两个小通项相等时的最小数,也就是最小值的S
例题:4-JJ78(三月84).ds某数除7余3,除4余2,求值。
解:设通项S=Am+B。由题目可知,必同时满足S=7a+3=4b+2
A同时可被7和4整除,为28(若是S=6a+3=4b+2,则A=12)
B为7a+3=4b+2的最小值,为10(a=1.b=2时,S有最小值10)

所以S=28m+10
满足这两个条件得出的通项公式,必定同时满足两个小通项。如果不能理解的话,就记住这个方法吧,此类的求通项的问题就能全部,一招搞定啦
第二种:X^n除以a余?类问题
解法见下图
特别说明:一种“个位循环”的解法是错误的,用该法做题很危险
4^50除以3的余数。
解:4^n的个位是以4、6两个数交替的周期为2的循环,根据个位循环法:4^50个位数为6,显然6能被3整除,所以余数“似乎”该为0.被3整除了?!但是4^50=2^100,根本没有3这个因子,不可能被3整除!
事实上:
4^50=(3+1)^50=>1^50除3的余数?=>余1
[b][size=4]好像我的例子举得有点问题。 [/b][/size] 这让很多G友都误解为一定要化为+1……
如果q^n都能化为k*p+1的形式,那大家直接猜余数为1好了……
我的想法是:化成“比该除数小的数”就行了
(注意,是小于除数的数注意该数的次幂!34L以及和想法相同的的同学)
请点击下载:
GMAT数学考试中余数精讲.doc
编辑推荐:
最新整理2013年4月GMAT机经考试全面解析(汇总)
2013.5最新整理GMAT机经考试真题全面讲解(汇总)
北京2013.5.19整理GRE机经考试真题全面回忆
更多信息请关注读书人网:www.Reader8.cn
GMAT:http://www.reader8.cn/exam/baojianyuan/频道!
 爱华网
爱华网