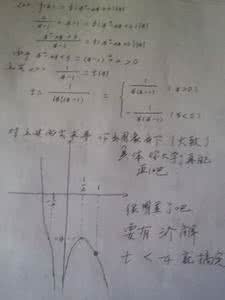
∵y=|x|为偶函数,y=x为奇函数
∴f(x)=x|x|奇函数
当x≥0时,f(x)=x2为增函数,由奇函数在对称区间上单调性相同可得
函数f(x)在R上增函数
又∵不等式f(x+2a)>4f(x)可化为(x+2a)|x+2a|>4x?|x|=2x?|2x|=f(2x)
故当x∈[a,a+1]时,不等式f(x+2a)>4f(x)恒成立,
即当x∈[a,a+1]时,不等式x+2a>2x恒成立
即x<2a恒成立
即a+1<2a
解得a>1
故实数a的取值范围是(1,+∞)
故答案为:(1,+∞)
考点:
考点名称:函数的奇偶性、周期性函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:
(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。
注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a,b均不为零,若:
(1)函数y=f(x)存在f(x)=f(x+a)==>函数最小正周期T=|a|
(2)函数y=f(x)存在f(a+x)=f(b+x)==>函数最小正周期T=|b-a|
(3)函数y=f(x)存在f(x)=-f(x+a)==>函数最小正周期T=|2a|
(4)函数y=f(x)存在f(x+a)===>函数最小正周期T=|2a|
(5)函数y=f(x)存在f(x+a)===>函数最小正周期T=|4a|
分段函数:
1、分段函数:定义域中各段的x与y的对应法则不同,函数式是分两段或几段给出的;
分段函数是一个函数,定义域、值域都是各段的并集。
抽象函数:
我们把没有给出具体解析式的函数称为抽象函数;
一般形式为y=f(x),或许还附有定义域、值域等,如:y=f(x),(x>0,y>0)。
知识点拨:
1、绝对值函数去掉绝对符号后就是分段函数。
2、分段函数中的问题一般是求解析式、反函数、值域或最值,讨论奇偶性单调性等。
3、分段函数的处理方法:分段函数分段研究。
 爱华网
爱华网