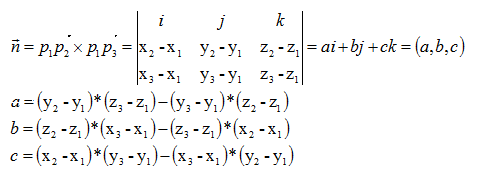考点：
考点名称：弧度制、弧度与角度的互化1弧度的角的概念：
长度等于半径长的弧所对的圆心角叫做1弧度的角，记作1rad。
弧度制：
用弧度作单位来度量角的制度叫弧度制。
一般地：正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0。
角α的弧度公式：
（l表示圆心角α所对的弧长，r表示圆的半径）。
角度与弧度的换算公式：
360°=2π，180°=π，1°=rad≈0.01745rad，1rad=≈57.30°=57°18′。
扇形面积公式：
S=lr=|α|r2。
原文地址：SAS中做蒙特卡洛模拟，根据已知对数正态分布，求符合该对数正态分布的随机数作者：庆可在SAS中没有直接产生对数正态分布随机数的函数。但是，我们可以通过以下公式转换来产生相应的对数正态分布随机数。例如：经检验以下数据经过检
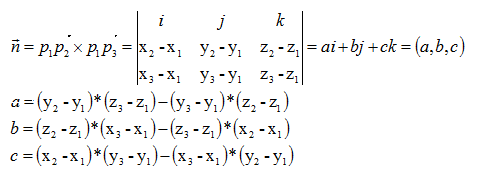
已知三点p1（x1,y1,z1），p2(x2,y2,z2)，p3(x3,y3,z3)，要求确定的平面方程关键在于求出平面的一个法向量，为此做向量p1p2（x2-x1,y2-y1,z2-z1),p1p3(x3-x1,y3-y1,z3-
里仁篇第十四章。 【原文】子曰：“不患无位，患所以立；不患莫已知，求为可知也。” 【注释】1、患－－－忧虑，怕。如：患得患失。2、位－－－地位。3、立－－－站得住脚。 【译文】孔子说：“不怕没有地位（或是官位）就怕自己没有学习到赖以站得住脚的东西；
不要简单模仿那些强势品牌的操作手法； 也不要迷信品牌靠“策划＋广告”就能做的出来； 从管理的角度建设你的品牌，而不是其他， 就好象从管家的角度去设计你的后花园，而不是从卖花匠的角度－－ 以传播做品牌的失效 如果要列
弦长公式，在这里指直线与圆锥曲线相交所得弦长d的公式。PS：圆锥曲线， 是数学、几何学中通过平切圆锥（严格为一个正圆锥面和一个平面完整相切）得到的一些曲线，如：椭圆，双曲线，抛物线等。在知道圆和直线方程求弦长时，可利用方法二，将直线方程代入
爱华网