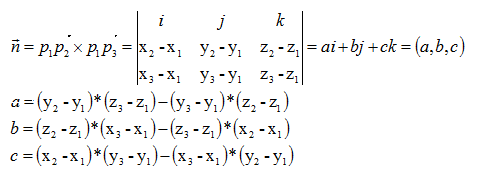已知焦点求椭圆方程 椭圆的标准方程 已知椭圆C的两焦点分别为，长轴长为6，（1）求椭圆C的标准方程；（2）已知过点（0，

考点：

直线与椭圆的方程：

设直线l的方程为：Ax+By+C=0（A、B不同时为零），椭圆（a＞b＞0），将直线的方程代入椭圆的方程，消去y（或x）得到一元二次方程，进而应用根与系数的关系解题。

椭圆的焦半径、焦点弦和通径：

（1）焦半径公式：
①焦点在x轴上时：|PF1|=a+ex0，|PF2|=a-ex0；
②焦点在y轴上时：|PF1|=a+ey0，|PF2|=a-ey0;
(2)焦点弦：
过椭圆焦点的弦称为椭圆的焦点弦．设过椭圆的弦为AB，其中A(x1，y1)，B(x2，y2)，则|AB|=2a+e(x1+x2)．由此可见，过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数．
(3)通径：过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆的通径，其长为

椭圆中焦点三角形的解法：

椭圆上的点与两个焦点F1，F2所构成的三角形，通常称之为焦点三角形，解焦点三角形问题经常使用三角形边角关系定理，解题中，通过变形，使之出现，这样便于运用椭圆的定义，得到a，c的关系，打开解题思路，整体代换求是这类问题中的常用技巧。

关于椭圆的几个重要结论：

（1）弦长公式：

（2）焦点三角形：
上异于长轴端点的点，
(3)以椭圆的焦半径为直径的圆必与以长轴为直径的圆内切．
(4)椭圆的切线：处的切线方程为

椭圆的标准方程：

（1）中心在原点，焦点在x轴上：；
（2）中心在原点，焦点在y轴上：。
椭圆的图像：

（1）焦点在x轴：
；
（2）焦点在y轴：
。

巧记椭圆标准方程的形式：

①椭圆标准方程的形式：左边是两个分式的平方和，右边是1；
②椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在哪一个轴上；
③椭圆的标准方程中，三个参数a，b，c满足a2= b2+ c2；
④由椭圆的标准方程可以求出三个参数a，b，c的值．

待定系数法求椭圆的标准方程：

求椭圆的标准方程常用待定系数法，要恰当地选择方程的形式，如果不能确定焦点的位置，那么有两种方法来解决问题：一是分类讨论，全面考虑问题；二是可把椭圆的方程设为n)用待定系数法求出m，n的值，从而求出标准方程，

爱华网本文地址 » http://www.aihuau.com/a/411751/738963061427.html