raoliu
绕流
flow past body
流体绕过置于无限流体中的物体的流动,或物体在无限流体中运动,是自然界和工程中常见的粘性流体流动形式。由于物体被流动流体所包围,常称为流动的外部问题。空气绕过机翼,水流绕过桥墩,船舶在海洋中航行,流体掠过换热管束,颗粒和液滴在气流中沉降,均属此类流动。
圆柱绕流特性 流体绕过物体流动时,流动特性因流体物理性质、物体形状和尺寸以及绕流速度等因素而有显著差异。典型的绕流是绕过长圆柱体的流动。在低雷诺数(例如<1时,这里=/;为来流速度;为圆柱直径;为流体运动粘度)的条件下,流动的主要特点是上下游速度分布对称(图1[低雷诺数绕流]),柱体影响流动所及的区域较广。
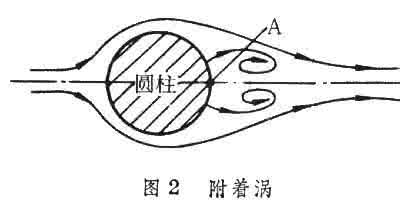
在中等雷诺数的条件下,上下游流速分布的对称性消失,绕圆柱附近流动的流体,在达到边缘中心点A之前离开圆柱,在圆柱体后面出现两个附着涡(图2[附着涡]),涡内流体不断循环,在一定条件下(如100>>40),圆柱两侧交替地发生旋涡发射,即在圆柱后的每一侧出现一排旋涡(图3[卡门涡街]),称为卡门涡街,这种交替发生的旋涡,导致周期性横向力的产生,迫使柱体振动。例如大气绕过高烟囱和高塔设备流动时,就会使其发生振动,并有可能造成危险。
在高雷诺数(>100)的条件下,柱体对绕流的影响限于表面附近的边界层中。此处速度梯度很大,粘性摩擦很显著。边界层之外,流体流速大体上即为来流速度,无速度梯度,粘性摩擦可以忽略。柱面上形成边界层后,在下游某处可能与柱面分离。当<3×10时,边界层内流体作层流流动,此为层流边界层;当>3×10时,边界层内的流动状态为湍流,湍流边界层的分离点向后移动。
绕流的速度分布 绕流时的速度分布,原则上可由运动方程计算,但由于非线性方程难以求解,须依照具体情况作出简化。对于绕圆球的流动,当<1时,速度分布可用下列方程表示:
[531-01]
[531-02]
[531-03]式中为沿方向的来流速度;、和各为和方向的速度分量;为球的半径;为离开坐标原点的距离;=++。当值较大时,可用边界层理论近似处理。
绕平板流动时层流边界层中的速度分布的精确解方程很复杂,可在无因次坐标图上表示(图4[平板边界层层流时速度分布])。纵坐标中为点速度;是距平板前缘的距离;是距平板的垂直距离。[kg1]和[kg2]分别为流体的密度和粘度。湍流边界层中的速度分布亦可用管流时的幂指数形式或对数形式表示,但相应的常数略有不同。
阻力定律 绕流的流动阻力包括摩擦阻力和压差阻力,其相对大小因物体形状、运动速度等因素而有差异。若被绕物体的几何形状比较简单,阻力可由边界层理论算出;当物体形状复杂时,阻力通常依靠实验测定,实验结果用阻力系数与雷诺数的关系表述。
绕平板流动的摩擦阻力、阻力系数[kg2]在层流时为:
[531-04]在湍流时则为:
=0.036(/)[531-1],=0.074[531-1]式中和分别为平板的宽度和长度。
绕球体作层流流动(<1)时,阻力可根据斯托克斯定律(1851年英国G.G.斯托克斯关于颗粒在流体中运动阻力)计算,即:
=3式中为球的直径。从这定律换算得出的阻力系数为:
=24
在高雷诺数(500<<2×10)时,阻力系数近似地为常数,阻力正比于速度的平方。在雷诺数更高时(>3×10),阻力系数急剧降低(图5[绕圆球时的阻力系数]),这是由于边界层湍流化,分离点后移,尾涡区缩小,因而使压差阻力大为降低。
戴干策
以上就是网友分享的关于"绕流"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网