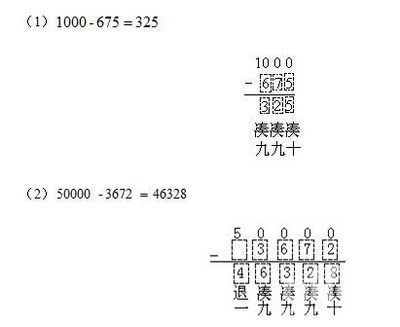
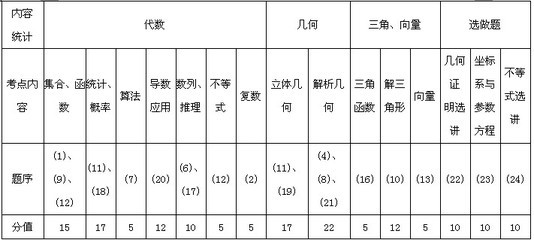
2012江苏高考数学试卷答案与解析
一.填空题:
1.已知集合A?{1,2,4},B?{2,4,6},则A?B?.
【答案】 ?1 ,2,4,6?
【解析】根据集合的并集运算,两个集合的并集就是所有属于集合A和集合B的元素组成的集合,从所给的两个集合的元素可知,它们的元素是1 ,2,4,6,所以答案为?1,2,4,6?.
【点评】本题重点考查集合的运算.容易出错的地方是审错题目,把并集运算看成交集运算.属于基本题,难度系数较小.
2. 某学校高一、高二、高三年级的学生人数之比为3:3:4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 ▲ 名学生.
【答案】15
【解析】根据分层抽样的方法步骤,按照一定比例抽取,样本容量为50,那么根据题意得:从高三一共可以抽取人数为:50?3?15人,答案 15 . 10
【点评】本题主要考查统计部分知识:抽样方法问题,分层抽样的具体实施步骤.分层抽样也叫做“按比例抽样”,也就是说,要根据每一层的个体数的多少抽取,这样才能够保证样本的科学性与普遍性,这样得到的数据才更有价值、才能够较精确地反映总体水平,本题属于容易题,也是高考热点问题,希望引起重视.
3. 设a,b?R,a?bi?
【答案】8
【解析】据题a?bi?
从而 a?b?8.
【点评】本题主要考查复数的基本运算和复数相等的条件运用,属于基本题,一定要注意审题,对于复数的除法运算,要切实掌握其运算技巧和常规思路,再者,需要注意分母实数化的实质.
4. 右图是一个算法流程图,则输出的k的值是.
11?7i(i为虚数单位),则a?b的值为 ▲ . 1?2i11?7i(11?7i)(1?2i)25?15i???5?3i,所以 a?5,b?3, 1?2i(1?2i)(1?2i)5
【答案】5
【解析】根据循环结构的流程图,当k?1时,此时k2?5k?4?0;不满足条件,继续执行循环体,当k?2时,k2?5k?4??6;不满足条件,继续执行循环,当k?3时,k2?5k?4??2不满足条件,然后依次出现同样的结果,当k?5时,此时k2?5k?4?4,此时满足条件跳出循环,输出k的值为5.
【点评】本题主要考查算法的定义、流程图及其构成,考查循环结构的流程图.注意循环条件的设置,以及循环体的构成,特别是注意最后一次循环的k的值.这是新课标的新增内容,也是近几年的常考题目,要准确理解循环结构流程图的执行过程.
5.
函数f(x)的定义域为.
【答案】 ?【解析】根据题意得到 1?2log6x?0,同时,x>0 ,解得log6x?
又x>0
,所以函数的定义域为: . 1,解得x?6,2?【点评】本题主要考查函数基本性质、对数函数的单调性和图象的运用.本题容易忽略x>0这个条件,因此,要切实对基本初等函——www.niubb.net——数的图象与性质有清晰的认识,在复习中应引起高度重视.本题属于基本题,难度适中.
6. 现有10个数,它们能构成一个以1为首项,?3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是 ▲ . 【答案】3 5
【解析】组成满足条件的数列为:1,?3,9.?27,81,?243,729,?2187,6561,?19683.从中随机
取出一个数共有取法10种,其中小于8的取法共有6种,因此取出的这个数小于8的概率为
3. 5
【点评】本题主要考查古典概型.在利用古典概型解决问题时,关键弄清基本事件数和基本事件总数,本题要注意审题,“一次随机取两个数”,意味着这两个数不能重复,这一点要特别注意.
7.如图,在长方体ABCD?A1B1C1D1中,AB?AD?3cm,AA1?2cm,则四棱锥A?BB1D1D的体积为 cm3.
【答案】6cm3
DA11 B1
C
D1A1
DA
O
B
C1B1
C
【解析】如图所示,连结AC交BD于点O,因为 平面ABCD?BB1D1D,又因为
AC?BD,所以,AC?平面BB1D1D,所以四棱锥A?BB1D1D的高为AO,根据题
意AB?AD?3cm,所
以AO?
32
,又因为BD?,AA1?2cm
,故矩形2
1BB1D1D的面积为2,
从而四棱锥A?BB1D1
D的体积V???6cm3.
3【点评】本题重点考查空间几何体的体积公式的运用.本题综合性较强,结合空间中点线面
的位置关系、平面与平面垂直的性质定理考查.重点找到四棱锥A?BB1D1D的高为AO,这是解决该类问题的关键.在复习中,要对空间几何体的表面积和体积公式记准、记牢,并且会灵活运用.本题属于中档题,难度适中.
x2y2
8. 在平面直角坐标系xOy中,若双曲线则m的值为 ▲ . ??1,mm2?
4
【答案】2
【解析】根据题目条件双曲线的焦点位置在x轴上(否则不成立),因此m>0,由离心率m?m2?4公式得到?5,解得 m?2 . m
【点评】本题考查双曲线的概念、标准方程和简单的几何性质.这是大纲中明确要求的,在对本部分复习时要注意:侧重于基本关系和基本理论性质的考查,从近几年的高考命题趋势看,几乎年年都有所涉及,要引起足够的重视.本题属于中档题,难度适中.
9. 如图,在矩形ABCD
中,AB?BC?2,点E为BC的中点,点F在边 CD
上,若????????????????AB?AF?AE?BF的值是.
【答案】2
【解析】根据题意AF?BC?DF,所以
???AB?AF?AB?(BC?DF)?AB?BC?AB?DF?AB?DF?AB?DFcos0????????????????从而得到DF?1,又因为AE?AD?DF,BF?BC?CF,所以
2??????
AE
?BF?(AD?DF)?(BC?CF)?BC?0?0?DF?CFcos180??2.
?????????
【点评】本题主要考查平面向量的基本运算,同时,结合平面向量的数量积运算解决.设法找到DF?1,这是本题的解题关键,本题属于中等偏难题目. ?
?1≤x?0,?ax?1,?10. 设f(x)是定义在R上且周期为2的函数,在区间[?1,1]上,f(x)??bx?2,0≤x≤1,??x?1
其中a,b?R.若f???f??,则a?3b的值为 ▲ .
【答案】?10 .
【解析】因为f???f??,函数f(x)的周期为2,所以 ?1??2??3??2??1?
?2??3??2?
131?得到3a?2b??2, f()?f( ?2)?f(?),根据f(x)??bx?2,0≤x≤1,222??x?1
又f(1)?f(?1),得到?a?1?
所以a?3b??10.
【点评】本题重点考查函数的性质、分段函数的理解和函数周期性的应用.利用函数的周期性将式子化简为f()?f(
题,难度适中.
11. 设?为锐角,若cos????1≤x?0,?ax?1,b?2,即2a?b?0,结合上面的式子解得a?2,b??4,21231?2)?f(?)然后借助于分段函数的解析式解决.属于中档22?
????4?,则sin(2??)的值为. ?6?512
【答案】172 50
?
?【解析】根据cos?????167??42, ?1???,cos(2??)?2cos(??)?1?2?6?5362525
24?7?,因为sin(2??)?1????325?25?因为cos(2???
3)?0,所以 ?2
sin(2???
12)?sin[(2???
3)??
4]?sin(2??
?3)cos?4?cos(2???3)sin?4?172. 50
【点评】本题重点考查两角和与差的三角公式、角的灵活拆分、二倍角公式的运用.在求解三角函数值时,要注意角的取值情况,切勿出现增根情况.本题属于中档题,运算量较大,难度稍高.
12. 在平面直角坐标系xOy中,圆C的方程为x2?y2?8x?15?0,若直线y?kx?2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是 ▲ . 【答案】4 3
2【解析】根据题意x2?y2?8x?15?0将此化成标准形式为:?x?4??y2?1,得到,该圆的
圆心为M?4,0?半径为1 ,若直线y?kx?2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,只需要圆心M?4,0?到直线y?kx?2的距离d?1?1,即可,所以有d?4k?2
k2?1?2,化简得k(3k?4)?0解得0?k?44,所以k的最大值是 . 33
【点评】本题主要考查直线与圆的位置关系、点到直线的距离公式、圆的一般式方程和标准方程的互化,考查知识较综合,考查转化思想在求解参数范围中的运用.本题的解题关键就是对若直线y?kx?2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,这句话的理解,只需要圆心M?4,0?到直线y?kx?2的距离d?1?1即可,从而将问题得以转化.本题属于中档题,难度适中.
b?R)的值域为[0,13. 已知函数f(x)?x2?ax?b(a,??),若关于x的不等式f(x)?c的
解集为(m,m?6),则实数c的值为 ▲ .
【答案】9
【解析】根据函数f(x)?x?ax?b?0,得到a2?4b?0,又因为关于x的不等式2
f(x)?c,可化为:x2?ax?b?c?0,它的解集为?m,m?6?,设函数f(x)?x2?ax?b?c图象与x轴的交点的横坐标分别为x1,x2,则x2?x1?m?6?m?6,从而,(x2?x1)2?36,即(x1?x2)2?4x1x2?36,又因为 x1x2?b?c,x1?x2??a,代入得 到 c?9.
【点评】本题重点考查二次函数、一元二次不等式和一元二次方程的关系,根与系数的关系.
二次函数的图象与二次不等式的解集的对应关系要理清.属于中档题,难度不大.
14. 已知正数a,b,c满足:5c?3a≤b≤4c?a,clnb≥a?clnc,则
【答案】?e,7?
【解析】
b的取值范围是 ▲ . a
【点评】本题主要考查不等式的基本性质、对数的基本运算.关键是注意不等式的等价变形,做到每一步都要等价——好文章——.本题属于中高档题,难度较大.
二、解答题
15. (本小题满分14分)
????????????????在?ABC中,已知AB?AC?3BA?BC.
(1)求证:tanB?3tanA;
(2
)若cosC?
【答案及解析】 求A的值.
【点评】本题主要考查向量的数量积的定义与数量积运算、两角和与差的三角公式、三角恒等变形以及向量共线成立的条件.本题综合性较强,转化思想在解题中灵活运用,注意两角和与差的三角公式的运用,考查分析问题和解决问题的能力,从今年的高考命题趋势看,几乎年年都命制该类型的试题,因此平时练习时加强该题型的训练.本题属于中档题,难度适中.
16. (本小题满分14分)
如图,在直三棱柱ABC?A1B1C1中,A1B1?A1C1,D,E分别是棱
(点D 不同于点C),且AD?DE, F为B1C1的中点.BC,CC1上的点
求证:(1)平面ADE?平面BCC1B1;
(2)直线A1F//平面ADE.
【答案及解析】
【点评】本题主要考查空间中点、线、面的位置关系,考查线面垂直、面面垂直的性质与判定,线面平行的判定.解题过程中注意中点这一条件的应用,做题规律就是“无中点、取中点,相连得到中位线”.本题属于中档题,难度不大,考查基础为主,注意问题的等价转化.
17. (本小题满分14分)
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y?kx?1(1?k2)x2(-好文章-k?0)表示的曲线上,其20
中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
【答案及解析】
【点评】本题主要考查二次函数的图象与性质以及求解函数最值问题.在利用导数求解函数的最值问题时,要注意增根的取舍,通过平面几何图形考查函数问题时,首先审清题目,然后建立数学模型,接着求解数学模型,最后,还原为实际问题.本题属于中档题,难度适中.
18.(本小题满分16分)
已知a,b是实数,1和?1是函数f(x)?x3?ax2?bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g?(x)?f(x)?2,求g(x)的极值点;
(3)设h(x)?f(f(x))?c,其中c?[?2,2],求函数y?h(x)的零点个数.
【答案及解析】
【点评】本题综合考查导数的定义、计算及其在求解函数极值和最值中的运用.考查较全面系统,要注意变形的等价性和函数零点的认识、极值和极值 点的理解.本题主要考查数形结合思想和分类讨论思想,属于中高档试题,难度中等偏上,考查知识比较综合,全方位考查分析问题和解决问题的能力,运算量比较大.
19. (本小题满分16分)
x2y2
如图,在平面直角坐标系xOy中,椭圆2?2?1(a?b?0)的左、右焦点分别为F1(?c,0),ab
?都在椭圆上,其中e为椭圆的离心率. e)和?eF2 (c,0).已知(1,
??(1)求椭圆的离心率;
(2)设A,B是椭圆上位于x轴上方的两点,且直线AF1 与直线BF2平行,AF2与BF1交于点P.
(i
)若AF1?BF2?AF1的斜率; (第19题) (ii)求证:PF1?PF2是定值.
【答案及解析】
【点评】本题主要考查椭圆的定义、几何性质以及直线与椭圆的关系.本题注意解题中,待定系数法在求解椭圆的标准方程应用,曲线和方程的关系.在利用条件AF1?BF2?时,需要注意直线AF1和直线BF2平行这个条件.本题属于中档题.
20. (本小题满分16分)
已知各项均为正数的两个数列{an}和{b
n}满足:an?1?6 2n?N?.
2????bbn???n(1)设bn?1?1?,n?N,求证:数列????是等差数列; aan???n???
(2
)设bn?1?【答案与解析】 bn,nwww.niubb.com?N?,且{an}是等比数列,求a1和b1的值. an

【点评】本题综合考查等差数列的定义、等比数列的有关知识的灵活运用、指数幂和根式的互化.数列通项公式的求解.注意利用等差数列的定义证明问题时一般思路和基本方法,本题是有关数列的综合题;从近几年的高考命题趋势看,数列问题仍是高考的热点 、重点问题,在训练时,要引起足够的重视.
数学Ⅱ(附加题)
21.[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若 .....................多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4 - 1:几何证明选讲](本小题满分10分)
如图,AB是圆O的直径,D,E为圆上位于AB异侧的两点,连结BD并延长至点C,
【答案与解析】
(第21-A题)
【点评】本题主要考查圆的基本性质,等弧所对的圆周角相等,同时结合三角形的基本性质考查.本题属于选讲部分,涉及到圆的性质的运用,考查的主要思想方法为等量代换法,属于中低档题,难度较小,从这几年的选讲部分命题趋势看,考查圆的基本性质的题目居多,在练习时,要有所侧重.
B.[选修4 - 2:矩阵与变换](本小题满分10分)
?13???44?,求矩阵A的特征值. 已知矩阵A的逆矩阵A?1???11????2??2?
【答案与解析】
【点评】本题主要考查矩阵的构成、矩阵的基本运算以及逆矩阵的求解、矩阵的特征多项式与特征值求解.在求解矩阵的逆矩阵时,首先分清求解方法,然后,写出相应的逆矩阵即可;在求解矩阵的特征值时,要正确的写出该矩阵对应的特征多项式,难度系数较小,中低档题.
C.[选修4 - 4:坐标系与参数方程](本小题满分10分 )
在极坐标中,已知圆C
经过点P
——http://www.niubb.net/——求圆C的极坐标方程.
【答案与解析】
???,圆心为直线?sin???34??
?
【点评】本题主要考查直线的参数方程和圆的参数方程、普通方程与参数方程的互化、两角和与差的三角函数.本题要注意已知圆的圆心是直线?sin(???
3)??3与极轴的交点,2
考查三角函数的综合运用,对于参数方程的考查,主要集中在常见曲线的考查上,题目以中低档题为主.
D.[选修4 - 5:不等式选讲](本小题满分10分)
已知实数x,y满足:|x?y|?
【答案与解析】
115,|2x?y|?,求证:|y|?. 3618
【点评】本题主要考查不等式的基本性质、绝对值不等式及其运用,属于中档题,难度适中.切实注意绝对值不等式的性质与其灵活运用.
22.(本小题满分10分)
设?为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,??0;当两条棱平行时,?的值为两条棱之间的距离;当两条棱异面时,??1.
(1)求概率P(??0);
(2)求?的分布列,并求其数学期望E(?).
【答案与解析】
【点评】本题主要考查概率统计知识:离散型随机变量的分布列、数学期望的求解、随机事件的基本运算.本题属于基础题目,难度中等偏上.考查离散型随机变量的分布列和期望的求解,在列分布列时,要注意?的取值情况,不要遗漏?的取值情况.
23.(本小题满分10分)
?设集合Pn?{1,2,…,n},n?N.记f(n)为同时满足下列条件的集合A的个数:
①A?Pn;②若x?A,则2x?A;③若x?ePnA,则2x?ePnA.
(1)求f(4);
(2)求f(n)的解析式(用n表示).
【答案与解析】
【点评】本题重点考查集合的概念、组成、元素与集合的基本关系、集合的基本运算—补
集和函数的解析式的求法.本题属于中档题,难 度适中.
 爱华网
爱华网