关键词:四元数 卡尔曼滤波 matlab 导航算法
中图分类号:TN967.2 文献标识码:A 文章编号:1007-9416(2016)11-0136-02
四轴飞行器是微型飞行器的其中一种,也是一种智能机器人。它利用有四个旋翼作为飞行引擎来进行空中飞行,它的尺寸较小、重量较轻、适合携带和使用的无人驾驶飞行器一样能够携带一定的任务载荷,具备自主导航飞行能力。在复杂、危险的环境下完成特定的飞行任务。飞行器姿态确定问题是飞行器导航中的关键性问题之一,常用的姿态误差模型主要有欧拉角模型、等效旋转矢量、四元数模型。其中四元数模型应用最广,然而由于目前主流的MEMS传感器(如mpu6000、6050、9050)只是将传感器测量到的数据输出,导致了量测噪声无法解决的问题,对此有人提出了融合滤波、互补滤波算法,改善了四元数量测噪声误差,但是这种算法本质上并没有解决噪声误差问题,并且反应速度稍慢,实时性不好。针对此,本文给出了一种卡尔曼滤波与四元数结合的算法,意在通过利用卡尔曼滤波使系统的实时性得到提高。
1 四元数与欧拉角的转换
1.1 欧拉角到四元数的转换
1.2 四元数到欧拉角的转换
2 卡尔曼滤波
2.1 卡尔曼滤波5个基本公式
X(k)=A X(k-1)+B U(k)+W(k) (1)
Z(k)=H X(k)+V(k) (2)
式(1-2)中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。A和B是系统参数,对于多模型系统,他们为矩阵。Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise),他们的covariance 分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。下面我们来用他们结合他们的covariances 来估算系统的最优化输出。首先我们要利用系统的过程模型,来预测下一状态的系统。假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:
X(k|k-1)=A X(k-1|k-1)+B U(k) (3)
P(k|k-1)=A P(k-1|k-1) A’+Q (4)
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) (5)
Kg(k)= P(k|k-1) H’/(H P(k|k-1) H’+R) (6)
P(k|k)=(I-Kg(k) H)P(k|k-1) (7)
式(3)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,如果没有控制量,它可以为0。式(4)中,P(k|k-1)是X(k|k-1)对应的covariance,P(k-1|k-1)是X(k-1|k-1)对应的covariance,A’表示A的转置矩阵,Q是系统过程的covariance。式(3-4)就是卡尔曼滤波器5个公式当中的前两个,也就是对系统的预测。式(5)其中Kg为卡尔曼增益(Kalman Gain)。式(6)已经得到了k状态下最优的估算值X(k|k)。但是为了要另卡尔曼滤波器不断的运行下去直到系统过程结束,我们还要更新k状态下X(k|k)的covariance。式(7)中I 为1的矩阵,对于单模型单测量,I=1。当系统进入k+1状态时,P(k|k)就是式子(4)的P(k-1|k-1)。这样,算法就可以自回归的运算下去。卡尔曼滤波器的原理基本描述了,式(3-6)和式(7)就是他的5个基本公式。
2.2 卡尔曼滤波的matlab的实现
我们假设状态的控制量U(k)为零:
z1=[0.7854,0.7854,0.7854,0.7854,0.7854,0.7854,0.7854,0.7854,0.7854,0.7854];
z2=[0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1];
z3=[0,0,0,0,0,0,0,0,0,0];
Pk__=[1,0,0;0,1,0;0,0,1];
A=eye(3);
Q=eye(3);
C=eye(3);
R=eye(3);
xk=[0,0,0]';
for k = 1:10
Pk_=A*Pk__*A'+Q;
Hk=Pk_*C'/(C*Pk_*C'+R);
zk=[z1(k);z2(k);z3(k)];
xk__=xk;
xk=A*xk__+Hk*(zk-C*A*xk__);
x1(k)=xk(1);
x2(k)=xk(2);
x3(k)=xk(3);
Pk=(eye(3)-Hk*C)*Pk_;
Pk__=Pk;
end
以上就是一个三维变量的卡尔曼滤波matlab代码对应的就是我们的传感器传递给我们的欧拉角:
q0=angle2quat(x1(0),x2(0),x3(0)) (8)
式(8)就是matlab的欧拉角转换四元数函数。
3 卡尔曼滤波和其他各种滤波算法的对比
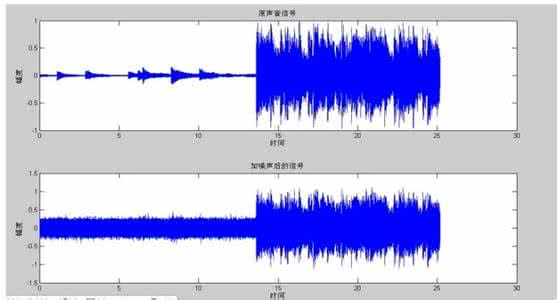
对比传统的算法,卡尔曼滤波有着更好的实时性,如图1所示是卡尔曼滤波和巴特沃斯低通滤波器等滤波算法的比较。这里均采用信号为Signal_Original_1=sin(2*pi*10*t)+sin(2*pi*20*t)+sin(2*pi*30*t);噪声为Noise_White_1= [0.3*randn(1,500),rand(1,500)]的信号叠加;则Mix_Signal_1= Signal_Original_1 + Noise_White_1。
4 结语
为了解决MEMS传感器传送数据实时性差的问题,本文提出了一种四元数和卡尔曼滤波组合的姿态结算方法,通过对MEMS传感器传送的数据进行卡尔曼滤波,降低数据误差,提高了四元数的实时性,针对四元数的卡尔曼滤波,本文给出了他的matlab实现,最后利用matlab软件进行仿真,实验结果表明:与传统数据算法相比,卡尔曼滤波算法在精度上有较大提高,算法的实时性有一定改善。
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网